
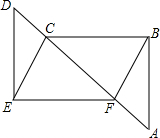
 如图,点A、F、C、D在同一条直线上,且AB=DE,BC=EF,AF=CD.
如图,点A、F、C、D在同一条直线上,且AB=DE,BC=EF,AF=CD.
|
|


科目:初中数学 来源: 题型:
 某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?
某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?查看答案和解析>>
科目:初中数学 来源: 题型:
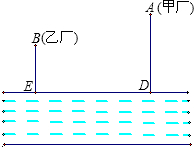 如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:
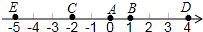 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com