练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在边长为1的小正方形组成的网格中，△ABC的顶点均在格点上，请按要求完成下列各题．

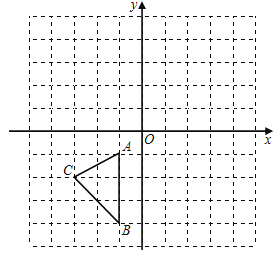
    （1）以原点O为对称中心作△ABC的中心对称图形，得到△A1B1C1，请画出△A1B1C1，并直接写出点A1，B1，C1的坐标；

    （2）求出△ABC的面积．

    【答案】（1）如图，△A1B1C1为所作，见详解；点A1，B1，C1的坐标分别为（1，﹣1），（1，4），（3，2）；（2）△ABC的面积为3．

    【解析】

    （1）作出△ABC各点关于原点的对称点，再顺次连接即可；根据平面直角坐标系写出A1，B1，C1三点的坐标即可．

    （2）利用三角形面积公式求面积即可.

    （1）如图，△A1B1C1为所作，点A1，B1，C1的坐标分别为（1，﹣1），（1，4），（3，2）；

    （2）△ABC的面积＝×2×3＝3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

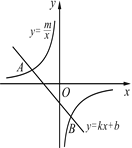
    【题目】如图，已知A(-4，2)、B(n，-4)是一次函数的图象与反比例函数的图象的两个交点．

    (1) 求反比例函数和一次函数的解析式；

    (2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知的面积是12，，点，分别在边，上，在边上依次作了个全等的小正方形，，，，，则每个小正方形的边长为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】截长补短法，是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或旋转等方式使两条短边拼合到一起，从而解决问题．

    （1）如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°，探索线段DA、DB、DC之间的数量关系．

    解题思路：将△ABD绕点A逆时针旋转60°得到△ACE，可得AE=AD, CE=BD，∠ABD=∠ACE,∠DAE=60°,根据∠BAC+∠BDC=180°,可知∠ABD+∠ACD=180°,则 ∠ACE+∠ACD=180°,易知△ADE是等边三角形，所以AD=DE，从而解决问题．

    根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________；

    （2）如图2,Rt△ABC中,∠BAC=90°,AB=AC．点D是边BC下方一点,∠BDC=90°，探索三条线段DA、DB、DC之间的等量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若抛物线（a、b、c是常数， ）与直线都经过轴上的一点P，且抛物线L的顶点Q在直线上，则称此直线与该抛物线L具有“一带一路”关系，此时，直线叫做抛物线L的“带线”，抛物线L叫做直线的“路线”．

    （1）若直线与抛物线具有“一带一路”关系，求m、n的值．

    （2）若某“路线”L的顶点在反比例函数的图象上，它的“带线” 的解析式为，求此路的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2－2x＋1

    （1）求此函数图象的顶点A以及它与y轴交点B的坐标．

    （2）求此函数图象与x轴的交点C和D的坐标；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

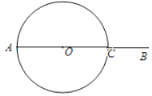
    【题目】如图，已知AB经过圆心O ，交⊙O于点C．

    （1）尺规作图：在AB上方的圆弧上找一点D，使得△ABD是以AB为底边的等腰三角形（保留作图痕迹）；

    （2）在（1）的条件下，若∠DAB=30°，求证：直线BD与⊙O相切．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

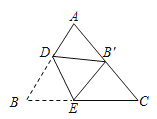
    【题目】如图，在△ABC中，AB＝AC＝5，BC＝6，点D，E分别在AB，BC上，将△ABC沿直线DE折叠，点B落在AC的中点B′处，则BE的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】制作一种产品，需先将材料加热达到60 ℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（min）．据了解，当该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加热前的温度为15 ℃，加热5分钟后温度达到60 ℃．

    （1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；

    （2）根据工艺要求，当材料的温度低于15 ℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？

    查看答案和解析>>

    同步练习册答案