
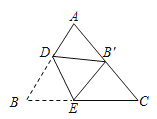
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D,E分别在AB,BC上,将△ABC沿直线DE折叠,点B落在AC的中点B′处,则BE的长为_____.
【答案】![]()
【解析】
如图,过点A作AH⊥BC,取CH中点F,连接B'F,由等腰三角形的性质和勾股定理可求AH=4,BH=CH=3,由三角形中位线定理可求B'F=![]() AH=2,CF=
AH=2,CF=![]() CH=
CH=![]() ,B'F∥AH,由勾股定理可求BE的长.
,B'F∥AH,由勾股定理可求BE的长.
解:如图,过点A作AH⊥BC,取CH中点F,连接B'F,
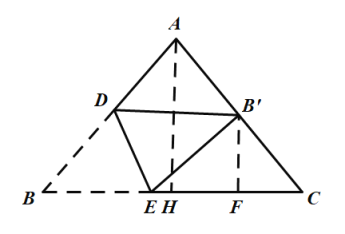
∵AB=AC=5,BC=6,AH⊥BC,
∴BH=HC=3,
∴AH=![]() ,
,
∵点B'是AC中点,点F是CH中点,
∴B'F=![]() AH=2,CF=
AH=2,CF=![]() CH=
CH=![]() ,B'F∥AH,
,B'F∥AH,
∴∠AHC=∠B'FC=90°,
∴BF=BC﹣CF=![]() ,
,
∵将△ABC沿直线DE折叠,点B落在AC的中点B′处,
∴BE=B'E,
∵B'E2=B'F2+EF2,
∴BE2=4+(![]() ﹣BE)2,
﹣BE)2,
∴BE=![]() ,
,
故答案为:![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
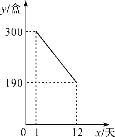
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题.
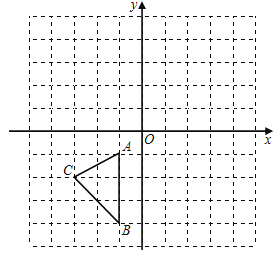
(1)以原点O为对称中心作△ABC的中心对称图形,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1,B1,C1的坐标;
(2)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点
的顶点![]() 在第一象限,过点
在第一象限,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴于点
轴于点![]() ,并交抛物线于点
,并交抛物线于点![]() .
.
(1)求抛物线![]() 顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围;
顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围;
(2)若直线![]() 交
交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且
,且![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=﹣![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.图象经过点(1,﹣3)
B.图象分布在第一、三象限
C.图象关于原点对称
D.图象与坐标轴没有交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春节,小娜家购买了4个灯笼,灯笼上分别写有“欢”、“度”、“春”、“节”(外观完全一样).
(1)小娜抽到“2019年”是 事件,“欢”字被抽中的是 事件;(填“不可能”或“必然”或“随机”).小娜从四个灯笼中任取一个,取到“春”的概率是 .
(2)小娜从四个灯笼中先后取出两个灯笼,请用列表法或画树状图法求小娜恰好取到“春”、“节”两个灯笼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
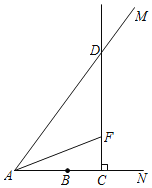
【题目】如图,射线![]() 上有一点
上有一点![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以每秒3个单位长度的速度沿射线
出发以每秒3个单位长度的速度沿射线![]() 运动,过点
运动,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,在射线
,在射线![]() 上取点
上取点![]() ,使得
,使得![]() ,连结
,连结![]() .设点
.设点![]() 的运动时间是
的运动时间是![]() (秒)(
(秒)(![]() ).
).
(1)当点![]() 在点
在点![]() 右侧时,求
右侧时,求![]() 、
、![]() 的长. (用含
的长. (用含![]() 的代数式表示)
的代数式表示)
(2)连结![]() ,设
,设![]() 的面积为
的面积为![]() 平方单位,求
平方单位,求![]() 与
与![]() 之间的丽数关系式.
之间的丽数关系式.
(3)当![]() 是轴对称图形时,直接写出
是轴对称图形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
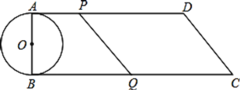
【题目】如图,在四边形ABCD中,AD//BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,
求:(1)t为何值时,P、Q两点之间的距离是10cm?
(2)t为何值时,直线PQ与⊙O相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有四个小球,上面分别标有数字﹣2,﹣1,0,1,它们除了数字不同外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是 .
(2)小聪先从袋子中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标;然后放回搅匀,接着小明从袋子中随机摸出一个小球,记下数字作为点M的纵坐标.如图,已知四边形ABCD的四个顶点的坐标分别为A(﹣2,0),B(0,﹣2),C(1,0),D(0,1),请用画树状图或列表法,求点M落在四边形ABCD所围成的部分内(含边界)的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com