
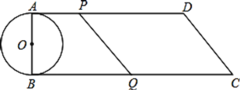
【题目】如图,在四边形ABCD中,AD//BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,
求:(1)t为何值时,P、Q两点之间的距离是10cm?
(2)t为何值时,直线PQ与⊙O相切?
【答案】(1)当t=5或8时, P、Q两点之间的距离是10cm;(2)t=8或![]() 时,直线PQ与⊙O相切
时,直线PQ与⊙O相切
【解析】
(1)作PE⊥BC于E,由勾股定理,得(264t)![]() +64=100,解得t=5或8问题得解;
+64=100,解得t=5或8问题得解;
(2)设运动t秒时,直线PQ与⊙O相切于点G,如图因为,AB=8,AP=t,BQ=26-3t,所以,PQ=26-2t,因而,过p做PH⊥BC,得HQ=26-4t,于是由勾股定理,可的关于t的一元二次方程,则t可求.问题得解.
(1)如图1,作PE⊥BC于E,
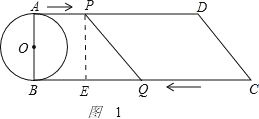
AP=t,BQ=263t,QE=264t.
由勾股定理,得(264t)![]() +64=100,
+64=100,
解得t=5或8;
∴当t=5或8时,P、Q两点之间的距离是10cm.
(2)设运动t秒时,直线PQ与⊙O相切于点G,过P作PH⊥BC于点H,
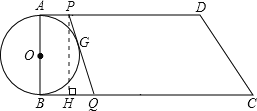
则PH=AB=8,BH=AP,
可得HQ=26-3t-t=26-4t,
由切线长定理得,AP=PG,QG=BQ,
则PQ=PG+QG=AP+BQ=t+26-3t=26-2t,
由勾股定理得:PQ2=PH2+HQ2,即(26-2t)2=82+(26-4t)2,
化简整理得 3t2-26t+16=0,
解得t=8或![]() ,
,
所以当t=8或![]() 时,直线PQ与⊙O相切.
时,直线PQ与⊙O相切.


科目:初中数学 来源: 题型:
【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:将△ABD绕点A逆时针旋转60°得到△ACE,可得AE=AD, CE=BD,∠ABD=∠ACE,∠DAE=60°,根据∠BAC+∠BDC=180°,可知∠ABD+∠ACD=180°,则 ∠ACE+∠ACD=180°,易知△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________;
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D,E分别在AB,BC上,将△ABC沿直线DE折叠,点B落在AC的中点B′处,则BE的长为_____.
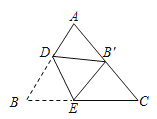
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售,从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
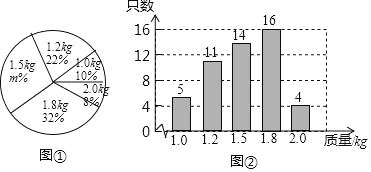
(1)图①中m的值为 ;
(2)这组数据的平均数是 kg,众数是 kg,中位数是 kg;
(3)根据样本数据,估计这2500只鸡中,质量为2.0kg的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
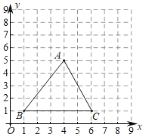
【题目】如图,由边长为1的小正方形构成的网格中,每个小正方形的顶点叫做格点,![]() 的顶点在格点上.
的顶点在格点上.
(1)直接写出![]() 的面积为 ;
的面积为 ;
(2)请用无刻度的直尺画出将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 角后得到的线段
角后得到的线段![]() ,并写出点
,并写出点![]() 的坐标为 ;
的坐标为 ;
(3)若一个多边形各点都不在⊙M外,则称⊙M全覆盖这个5多边形,已知点![]() ,⊙M全覆盖四边形
,⊙M全覆盖四边形![]() ,则⊙M的直径最小为
,则⊙M的直径最小为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种产品,其标价比进价每件多![]() 元,且商店用
元,且商店用![]() 元购进这种商品的数量和这种商品
元购进这种商品的数量和这种商品![]() 元的销售额所售出的件数相同.
元的销售额所售出的件数相同.
![]() 求这种商品的进价及标价;
求这种商品的进价及标价;
![]() 经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出
经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出![]() 件,每涨价
件,每涨价![]() 元,则少卖出
元,则少卖出![]() 件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com