
【题目】已知抛物线![]() 的顶点
的顶点![]() 在第一象限,过点
在第一象限,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴于点
轴于点![]() ,并交抛物线于点
,并交抛物线于点![]() .
.
(1)求抛物线![]() 顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围;
顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围;
(2)若直线![]() 交
交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且
,且![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
【答案】(1)函数解析式为y=x+4(x>0);(2)0≤S≤![]() .
.
【解析】
(1)抛物线解析式为y=-x2+2mx-m2+m+4,设顶点的坐标为(x,y),利用抛物线顶点坐标公式得到x=m,y=m-4,然后消去m得到y与x的关系式即可.
(2)如图,根据已知得出OE=4-2m,E(0,2m-4),设直线AE的解析式为y=kx+2m-4,代入A的坐标根据待定系数法求得解析式,然后联立方程求得交点P的坐标,根据三角形面积公式表示出S=![]() (4-2m)(m-2)=-m2+3m-2=-(m-
(4-2m)(m-2)=-m2+3m-2=-(m-![]() )2+
)2+![]() ,即可得出S的取值范围.
,即可得出S的取值范围.
(1)由抛物线y=-x2+2mx-m2+m+4可知,a=-1,b=2m,c=-m2+m+4,
设顶点的坐标为(x,y),
∴x=-![]() =m,
=m,
∵b=2m,
y=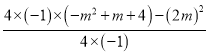 =m+4=x+4,
=m+4=x+4,
即顶点的纵坐标随横坐标变化的函数解析式为y=x+4(x>0);
(2)如图,由抛物线y=-x2+2mx-m2+m+4可知顶点A(m,m+4),
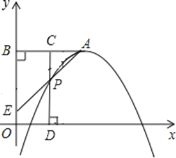
∵![]() 轴
轴
∴![]() 轴
轴
∴△ACP∽△ABE,
∴![]()
∵![]()
∴![]() ,
,
∵AB=m,
∴BE=2m,
∵OB=4+m,
∴OE=4+m-2m=4-m,
∴E(0,4-m),
设直线AE的解析式为y=kx+4-m,
代入A的坐标得,m+4=km+4-m,解得k=2,
∴直线AE的解析式为y=2x+4-m,
解![]()
得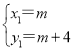 ,
,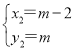 ,
,
∴P(m-2,m),
∴S=![]() (4-m)(m-2)=-m2+3m-2=-
(4-m)(m-2)=-m2+3m-2=-![]() (m-3)2+
(m-3)2+![]() ,
,
∴S有最大值![]() ,
,
∴△OEP的面积S的取值范围:0≤S≤![]() .
.


科目:初中数学 来源: 题型:
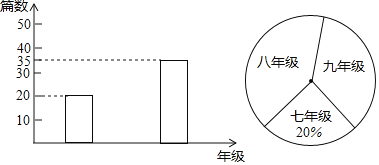
【题目】池州十中组织七、八、九年级学生参加“中国梦”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了以下两幅不完整的统计图,根据图中提供的信息完成以下问题:
(1)全校参赛作文篇数为 篇,补全条形统计图;
(2)扇形统计图中九年级参赛作文篇数对应的圆心角是 ;
(3)经过评审,全校共有4篇作文荣获一等奖,其中一篇来自七年级,两篇来自八年级,一篇来自九年级,学校准备从一等奖作文中任选两篇刊登在校刊上,请用树状图方法求出九年级一等奖作文登上校刊的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:将△ABD绕点A逆时针旋转60°得到△ACE,可得AE=AD, CE=BD,∠ABD=∠ACE,∠DAE=60°,根据∠BAC+∠BDC=180°,可知∠ABD+∠ACD=180°,则 ∠ACE+∠ACD=180°,易知△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________;
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
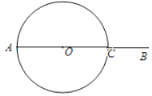
【题目】如图,已知AB经过圆心O ,交⊙O于点C.
(1)尺规作图:在AB上方的圆弧上找一点D,使得△ABD是以AB为底边的等腰三角形(保留作图痕迹);
(2)在(1)的条件下,若∠DAB=30°,求证:直线BD与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:如何计算平面直角坐标系中任意两点之间的距离?
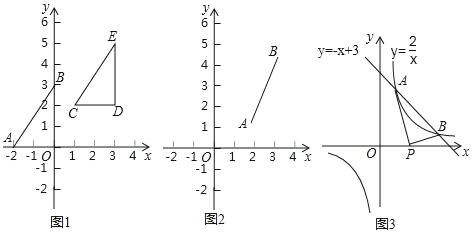
探究问题:
为解决上面的问题,我们从最简单的问题进行研究.
探究一:在图1中,已知线段AB,A(﹣2,0),B(0,3),写出线段AO的长,BO的长,所以线段AB的长为多少;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE,写出Rt△CDE的顶点坐标C,D,E,此时线段CD的长为多少,DE的长为多少,所以线段CE的长为多少.
探究二:在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长(用含a,b,c,d的代数式表示,不必证明).
归纳总结:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(x1,y1),B(x2,y2)时线段AB的长为多少(用含x1,y1,x2,y2的代数式表示,不必证明).
拓展与应用:
运用在图3中,一次函数y=﹣x+3与反比例函数y=![]() 的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
①求线段AB的长;
②若点P是x轴上动点,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
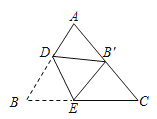
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D,E分别在AB,BC上,将△ABC沿直线DE折叠,点B落在AC的中点B′处,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种产品,其标价比进价每件多![]() 元,且商店用
元,且商店用![]() 元购进这种商品的数量和这种商品
元购进这种商品的数量和这种商品![]() 元的销售额所售出的件数相同.
元的销售额所售出的件数相同.
![]() 求这种商品的进价及标价;
求这种商品的进价及标价;
![]() 经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出
经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出![]() 件,每涨价
件,每涨价![]() 元,则少卖出
元,则少卖出![]() 件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com