
【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为16米,拱高(CD)为4米,求:
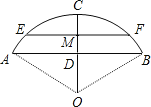
(1)桥拱半径.
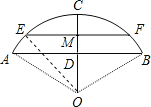
(2)若大雨过后,桥下河面宽度(EF)为12米,求水面涨高了多少?
【答案】(1)10m;(2)2m.
【解析】
(1)由垂径定理可求得AD的长度,OD=OC-CD,AO=CO,在Rt△ADO中,利用勾股定理求得桥拱半径AO;(2)求水面涨高了多少实际是求DM的长度,建立直角三角形,连接EO,EF=12,由垂径定理求得EM长,利用勾股定理把MO求出来,因为CO,CD已知,所以OD可求,OM-OD即为所求DM长.
(1)∵拱桥的跨度AB=16m,∴AD=8m,
因为拱高CD=4m,利用勾股定理可得:AO2-(OC-CD)2=82,
解得OA=10(m).
所以桥拱半径为10m;
(2)设河水上涨到EF位置(如图所示),
这时EF=12m,EF∥AB,有OC⊥EF(垂足为M),
∴EM=![]() EF=6m,
EF=6m,
连接OE,则有OE=10m,
OM2=OE2-EM2=102-62=64,
所以OM=8(m)OD=OC-CD=10-4=6(m),OM-OD=8-6=2(m).
即水面涨高了2m.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α。
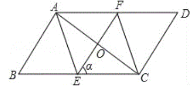
(1)当α的度数是_________时,四边形AFCE为菱形;
(2)当α的度数是_________时,四边形AFCE为矩形;
(3)四边形AFCE能否为正方形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
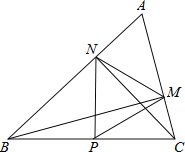
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=![]() PC.其中正确的个数是()
PC.其中正确的个数是()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
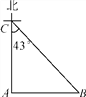
【题目】如图,海面上B,C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A,B两岛之间的距离.(结果精确到0.1海里)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
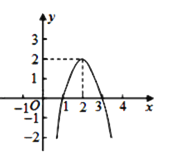
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应潜江市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
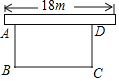
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
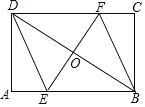
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com