
【题目】如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α。
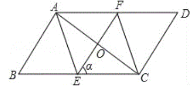
(1)当α的度数是_________时,四边形AFCE为菱形;
(2)当α的度数是_________时,四边形AFCE为矩形;
(3)四边形AFCE能否为正方形?为什么?
【答案】(1)60;(2)30;(3)不能
【解析】
(1)当α的度数是60°时,四边形AFCE为菱形,首先证明四边形AFCE、四边形AFEB是平行四边形,再证明△ABE是等边三角形即可解决问题.
(2)当α的度数是30°时,四边形AFCE为矩形,取BC中点M,连接AM,首先证明△ABM是等边三角形,推出∠OCE=30°即可解决问题.
(3)不可能,只要证明AE≠AF即可解决问题.
(1)当α的度数是60°时,四边形AFCE为菱形,理由如下:
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAO=∠ECO.
在△AOF和△COE中,∵ ,∴△AOF≌△COE(ASA),∴OE=OF.
,∴△AOF≌△COE(ASA),∴OE=OF.
∵OA=OC,∴四边形AFCE是平行四边形,∴AF=CE,AF∥BC,∴AF∥BE.
∵∠α=∠ABC=60°,∴AB∥EF,∴四边形AFEB是平行四边形,∴AF=BE=CE.
∵BC=8,AB=4,∴AB=BE=4.
∵∠B=60°,∴△ABE是等边三角形,∴AE=BE=CE.
∵四边形AFCE是平行四边形,∴四边形AFCE是菱形.
故答案为:60°;

(2)当α的度数是30°时,四边形AFCE为矩形,理由如下:
同(1)得:四边形AFCE是平行四边形,取BC中点M,连接AM.
∵AB=BM=4,∠B=60°,∴△ABM是等边三角形,∴∠AMB=60°,AM=BM=AB=CM,∴∠ACM=∠MAC=30°.
∵∠α=30°,∴∠OEC=∠OCE,∴OE=OC.
∵OE=OF,OA=OC,∴AC=EF,∴四边形AECF是矩形.
故答案为:30°.
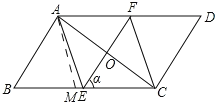
(3)四边形AECF不可能是正方形.
理由如下:如图四边形AFCE是矩形.
∵AB=4,BC=8,∠B=60°,∴在Rt△ABF中,AF=ABsin∠B=2![]() ,BF=ABcos60°=2,∴CF=BC﹣BF=8﹣2=6.
,BF=ABcos60°=2,∴CF=BC﹣BF=8﹣2=6.
∵AF≠FC,∴四边形AFCE不是正方形.


科目:初中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() .与
.与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上.
上.
(1)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(2)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为
的增大而增大的部分为![]() ,直线
,直线![]() 向下平移
向下平移![]() 个单位,当平移后的直线与
个单位,当平移后的直线与![]() 有公共点时,求
有公共点时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店以每件40元的价格购进一批衬衫,在试销过程中发现:每月销售量y(件)与销售单价x(x为正整数)(元)之间符合一次函数关系,当销售单价为55元时,月销售量为140件;当销售单价
为70元时,月销售量为80件.
(1)求y与x的函数关系式;
(2)如果每销售一件衬衫需支出各种费用1元,设服装店每月销售该种衬衫获利为w元,求w与x之间的函数关系式,并求出销售单价定为多少元时,商场获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C. D. E三点不在同一直线上时,以ED、EC我邻边作ECFD,设点D运动的时间为t(秒).
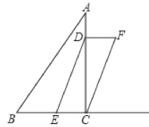
(1)用含t的代数式表示CE的长度。
(2)当F点落在△ABC的内部时,求t的取值范围。
(3)设ECFD的面积为S(平方单位),求S与t之间的函数关系式。
(4)当点F到Rt△ABC的一条直角边的距离是到另一条直角边距离的2倍时,直接写出ECFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】整数a满足下列两个条件,使不等式﹣2≤![]() <
<![]() a+1恰好只有3个整数解,使得分式方程
a+1恰好只有3个整数解,使得分式方程![]() =1的解为整数,则所有满足条件的a的和为( )
=1的解为整数,则所有满足条件的a的和为( )
A. 2B. 3C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组对函数y=|x2﹣2x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围取足全体实数,x与y的几组对应值列表如下:其中m= .
x | …… | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | …… |
y | …… | 3 | m | 0 | 0.75 | 1 | 0.75 | 0 | 1.25 | 3 | …… |
(2)根括上表数据,在如图所示的平面直角坐标系中描点,现在画出了函数图象的一部分,请画出该函数图象的另一部分.
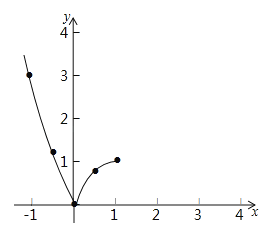
(3)观察函数图象,写出函数的一条性质 ;
(4)进一步探究函数图象解决问题:
①方程|x2﹣2x|=![]() 有 个实数根;
有 个实数根;
②在(2)问的平面直角坐标系中画出直线y=﹣x+1,根据图象写出方程|x2﹣2x|=﹣x+1的一个正数根约为 .(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).

(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为16米,拱高(CD)为4米,求:
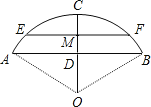
(1)桥拱半径.
(2)若大雨过后,桥下河面宽度(EF)为12米,求水面涨高了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com