
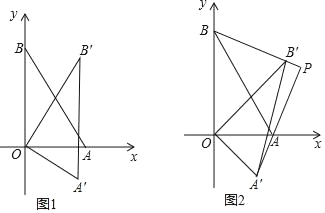
【题目】在平面直角坐标系中,已知点A(2,0),点B(0,2![]() ),点O(0,0).△AOB绕着O顺时针旋转,得△A′OB′,点A、B旋转后的对应点为A′、B′,记旋转角为α.
),点O(0,0).△AOB绕着O顺时针旋转,得△A′OB′,点A、B旋转后的对应点为A′、B′,记旋转角为α.
(I)如图1,若α=30°,求点B′的坐标;
(Ⅱ)如图2,若0°<α<90°,设直线AA′和直线BB′交于点P,求证:AA′⊥BB′;
(Ⅲ)若0°<α<360°,求(Ⅱ)中的点P纵坐标的最小值(直接写出结果即可).
【答案】(1)B'的坐标为(![]() ,3);(2)见解析 ;(3)
,3);(2)见解析 ;(3)![]() ﹣2.
﹣2.
【解析】
(1)设A'B'与x轴交于点H,由OA=2,OB=2![]() ,∠AOB=90°推出∠ABO=∠B'=30°,
,∠AOB=90°推出∠ABO=∠B'=30°,
由∠BOB'=α=30°推出BO∥A'B',由OB'=OB=2![]() 推出OH=
推出OH=![]() OB'=
OB'=![]() ,B'H=3即可得出;
,B'H=3即可得出;
(2)证明∠BPA'=90![]() 即可;
即可;
(3)作AB的中点M(1,![]() ),连接MP,由∠APB=90°,推出点P的轨迹为以点M为圆心,以MP=
),连接MP,由∠APB=90°,推出点P的轨迹为以点M为圆心,以MP=![]() AB=2为半径的圆,除去点(2,
AB=2为半径的圆,除去点(2,![]() ),所以当PM⊥x轴时,点P纵坐标的最小值为
),所以当PM⊥x轴时,点P纵坐标的最小值为![]() ﹣2.
﹣2.
(Ⅰ)如图1,设A'B'与x轴交于点H,
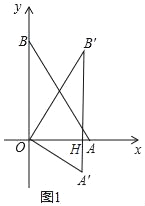
∵OA=2,OB=2![]() ,∠AOB=90°,
,∠AOB=90°,
∴∠ABO=∠B'=30°,
∵∠BOB'=α=30°,
∴BO∥A'B',
∵OB'=OB=2![]() ,
,
∴OH=![]() OB'=
OB'=![]() ,B'H=3,
,B'H=3,
∴点B'的坐标为(![]() ,3);
,3);
(Ⅱ)证明:∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',
∴∠OBB'=∠OA'A=![]() (180°﹣α),
(180°﹣α),
∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,
∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,
即AA'⊥BB';
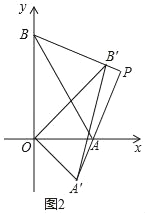
(Ⅲ)点P纵坐标的最小值为![]() .
.
如图,作AB的中点M(1,![]() ),连接MP,
),连接MP,
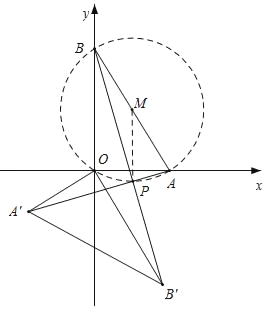
∵∠APB=90°,
∴点P的轨迹为以点M为圆心,以MP=![]() AB=2为半径的圆,除去点(2,
AB=2为半径的圆,除去点(2,![]() ).
).
∴当PM⊥x轴时,点P纵坐标的最小值为![]() ﹣2.
﹣2.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】吃香肠是庐江县春节的传统习俗,小严的父亲去年春节前用了![]() 元购买猪肉装香肠;今年下半年受非洲猪瘟影响,猪肉出现大幅度涨价,价格比去年上涨了
元购买猪肉装香肠;今年下半年受非洲猪瘟影响,猪肉出现大幅度涨价,价格比去年上涨了![]() 元
元![]() ,
,
(1)如果去年猪肉价格为![]() 元
元![]() ,求今年
,求今年![]() 元比去年少买多少
元比去年少买多少![]() 猪肉?(结果用
猪肉?(结果用![]() 的式子表示)
的式子表示)
(2)近期县政府为保障猪肉市场供应,为百姓生活着想,采取一系列惠民政策,猪肉价格下降了![]() 元
元![]() ,这样小严的父亲花了
,这样小严的父亲花了![]() 买到和去年一样多的猪肉.求小严父亲今年购买猪肉每千克多少元.
买到和去年一样多的猪肉.求小严父亲今年购买猪肉每千克多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
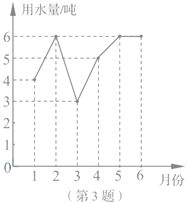
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
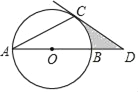
【题目】如图,AB是圆O的直径,AC是圆O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=2![]() .
.
(1)求∠A的度数.
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校冬季趣味运动会开设了“抢收抢种”项目,八(5)班甲、乙两个小组都想代表班级参赛,为了选择一个比较好的队伍,八(5)班的班委组织了一次选拔赛,甲、乙两组各10人的比赛成绩如下表:
甲组 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙组 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲组成绩的中位数是 分,乙组成绩的众数是 分.
(2)计算乙组的平均成绩和方差.
(3)已知甲组成绩的方差是1.4,则选择 组代表八(5)班参加学校比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强在做课后习题时,遇到这样一道题:“如图所示,![]() 、
、![]() 两村庄在一条河的两岸,从
两村庄在一条河的两岸,从![]() 村庄去
村庄去![]() 村庄,需要在河上造一座桥
村庄,需要在河上造一座桥![]() ,请问桥造在何处从
,请问桥造在何处从![]() 村庄去
村庄去![]() 村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
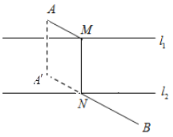
小强的解题思路,因为桥与河岸垂直,线段![]() 是一个不变的量,将它平移到
是一个不变的量,将它平移到![]() 处得线段
处得线段![]() ,总的路程
,总的路程![]() 与
与![]() 是相等的,故要使
是相等的,故要使![]() 最短,就是求点
最短,就是求点![]() 到点
到点![]() 最短即可,所以点
最短即可,所以点![]() 应是
应是![]() 与
与![]() 的交点.根据上述材料解答下列问题:如图所示:
的交点.根据上述材料解答下列问题:如图所示:![]() 、
、![]() 两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从
两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从![]() 地出发到
地出发到![]() 地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河
地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河![]() 与
与![]() 的宽为
的宽为![]() ,河
,河![]() 与
与![]() 的宽为
的宽为![]() ).
).
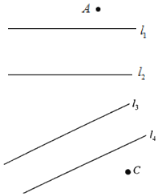
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com