
【题目】计算:3x(4y+1)的结果为_______________
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如下表:
第一次 | 第二次 | |
甲种货车辆数(辆) | 2 | 5 |
乙种货车辆数(辆) | 3 | 6 |
累计运货吨数(吨) | 15.5 | 35 |
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是。
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
频数 | 9 | 15 | ? | 16 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1-1,要在燃气管道l上修建一个泵站,分别向A,B两城镇供气泵站修在什么地方,可使所用的输气管线最短?
(2)如图1-2,公园内两条小河汇合,两河形成的半岛上有一处古迹P,现计划在两条小河上各修建一座小桥(垂直于河岸),并在半岛上修三条小路,连通两座小桥与古迹,这两座小桥应建在何处,使修路的费用最少?
(3)如图1-3,公园中有两处古迹P和Q,现计划在两条小河上各修建一座小桥(垂直于河岸),并在半岛上修四条小路,连通两座小桥与古迹,这两座小桥应建在何处,才能使修路的费用最少?
(4)如图1-4,现有一条地铁线路l,小区A和小区B在l的同侧,已知地铁站两入口C、D间的长度为a米,现设计两条路AC、BD连接入口和两小区地铁站入口C、D设计在何处,能使得修建公路AC与BD的费用和最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
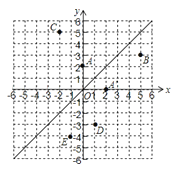
【题目】如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′ 、C′ ;
(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为 ;
(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线L上画出点Q,使△QDE的周长最小,并求△QDE周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD. 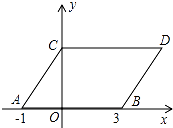
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图是随机抽查了某个地区的20个家庭的收入情况绘制而成,下列说法正确的是( )
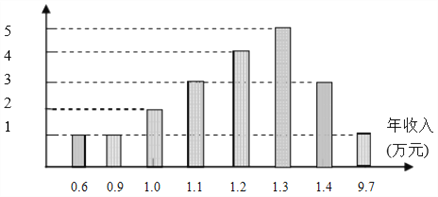
A. 这20个家庭的年平均收入为2.15万元 B. 这组数据的中位数是1.15万元
C. 这组数据的众数是1.3万元 D. 这组数据的众数是5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】资料显示,目前入驻天猫的商户,销售额中:广告费占比15%~20% ,物流费占比5%~8%,平台佣金费占比5%,仓库配货费占比5%,人员工工资占比10%.若其它成本占销售额的50%,则商户的利润约为销售额的( )
A. 2%~10% B. 40%~48% C. 10%~20% D. 12%~20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解下面内容,并解决问题:
据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根,华罗庚脱口而出地报出答案,邻座的乘客十分惊奇,忙问计算的奥秘.
(1)由103=1000,1003=1000000,你能确定![]() 是几位数吗?
是几位数吗?
∵1000<59319<1000000,
∴10<![]() <100.
<100.
∴![]() 是两位数;
是两位数;
(2)由59319的个位上的数是9,你能确定![]() 的个位上的数是几吗?
的个位上的数是几吗?
∵只有个位数是9的立方数是个位数依然是9,
∴![]() 的个位数是9;
的个位数是9;
(3)如果划去59319后面的三位319得到59,而33=27,43=64,由此你能确定![]() 的十位上的数是几吗?
的十位上的数是几吗?
∵27<59<64,
∴30<![]() <40.
<40.
∴![]() 的十位数是3.
的十位数是3.
所以, ![]() 的立方根是39.
的立方根是39.
已知整数50653是整数的立方,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com