
分析 (1)将m=1代入二次函数的解析式,然后利用配方法求解即可;
(2)将x=-1代入函数的解析式,令y>1即可求得m的取值范围.
解答 解:(1)∵m=1,
∴二次函数y=x2-2x+3=(x-1)2+2.
∵a=1>0,
∴抛物线开口向上,y有最小值,最小值为2.
(2)将x=0代入得:y=3,由抛物线的性质可知:当x=-1时,y>1,则函数y的值恒大于1.
将x=-1代入得:y=4+2m.则4+2m>1.
解得:m>-$\frac{3}{2}$.
当对称轴x=m在-1与0之间时,顶点(m,-m2+3)的纵坐标大于1满足条件,
故m的取值范围是m>-$\frac{3}{2}$.
点评 本题主要考查的是二次函数的性质和二次函数的最值,掌握二次函数的性质是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
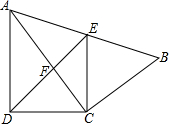 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com