
【题目】如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.
(1)箱盖绕点A转过的角度为______,点B到墙面的距离为______cm;
(2)求箱子的宽EF(结果保留整数,可用科学计算器).(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
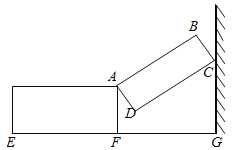
【答案】(1)150°;5(2)32.4cm
【解析】
(1)如图,过点B作BH⊥CG于H,过点D作CG的垂线MN交AF于M,交HG于N.利用矩形的性质、直角三角形的性质以及等角的余角相等得到∠MAD=30°,根据周角的定义易求箱盖绕点A转过的角度;通过解直角△BHC来求BH的长度;
(2)通过解直角△AMD得到线段MD的长度,则DN=65-EF-DM,利用解直角△DCN来求CD的长度,即EF的长度即可.
(1)如图,过点B作BH⊥CG于H,过点D作CG的垂线MN交AF于M,交HG于N.
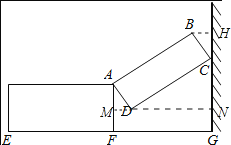
∵∠DCG=60°,
∴∠CDN=30°.
又∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,
∴∠MAD=∠CDN=30°(同角的余角相等),
∴箱盖绕点A转过的角度为:360°-90°-30°-90°=150°.
在直角△BCH中,∠BCH=30°,BC=10cm,则BH=![]() BC=5cm.
BC=5cm.
故答案是:150°;5;
(2)在直角△AMD中,AD=BC=10cm,∠MAD=30°,则MD=ADsin30°=![]() ×10=5(cm).
×10=5(cm).
∵∠CDN=30°,
∴cos∠CDN=cos30°=![]() ,即
,即![]()
解得EF=32.4.
即箱子的宽EF是32.4cm.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
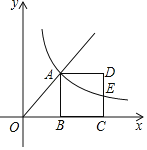
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
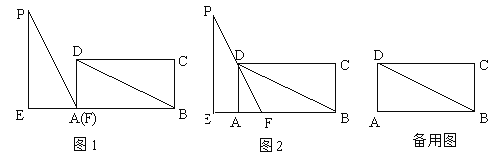
【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.

(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.
中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.

(1)求![]() 的度数.
的度数.
(2)如图,点E在⊙O上,连接CE与⊙O交于点F,若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com