
【题目】如图,在□ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在点B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G。

求证:(1)∠1=∠2 (2)DG=B′G
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学校数学兴趣小组利用机器人开展数学活动.在相距![]() 个单位长度的直线跑道
个单位长度的直线跑道![]() 上,机器人甲从端点
上,机器人甲从端点![]() 出发,匀速往返于端点
出发,匀速往返于端点![]() 、
、![]() 之间,机器人乙同时从端点
之间,机器人乙同时从端点![]() 出发,以大于甲的速度匀速往返于端点
出发,以大于甲的速度匀速往返于端点![]() 、
、![]() 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
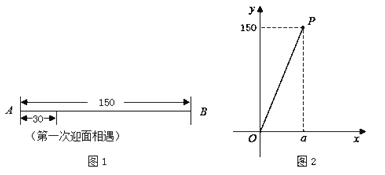
(观察)
①观察图![]() ,若这两个机器人第一次迎面相遇时,相遇地点与点
,若这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,则他们第二次迎面相遇时,相遇地点与点
个单位长度,则他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为 _____个单位长度;
之间的距离为 _____个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,则他们第二次迎面相遇时,相遇地点与点
个单位长度,则他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为 _____个单位长度;
之间的距离为 _____个单位长度;
(发现)
设这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,他们第二次迎面相遇时,相遇地点与点
个单位长度,他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度.兴趣小组成员发现了
个单位长度.兴趣小组成员发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图
,如图![]() 所示).
所示).
①![]() = _____;
= _____;
②分别求出各部分图象对应的函数表达式,并在图![]() 中补全函数图象;
中补全函数图象;
(拓展)
设这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,他们第三次迎面相遇时,相遇地点与点
个单位长度,他们第三次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点
个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点![]() 之间的距离
之间的距离![]() 不超过
不超过![]() 个单位长度,则他们第一次迎面相遇时,相遇地点与点
个单位长度,则他们第一次迎面相遇时,相遇地点与点![]() 之间的距离
之间的距离![]() 的取值范围是 _____.(直接写出结果)
的取值范围是 _____.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期 | 29日 | 30日 | 5月1日 | 2日 | 3日 | 4日 | 5日 |
日最高气温 | 16°C | 19°C | 22°C | 24°C | 26°C | 24°C | 23°C |
A. 24,23,10B. 24,23,![]() C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小明和小亮两名运动员中挑出一人参加立定跳远比赛,学校记录了二人在最近的6次立定跳远选拔赛中的成绩(单位:cm),并进行整理、描述和分析.下面给出了部分信息.
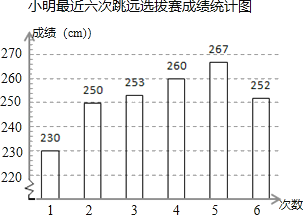
a.如图
b.小亮最近6次选拔赛成绩如下:
250 | 254 | 260 | 271 | 255 | 240 |
c.小明和小亮最近6次选拔赛中成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
小明 | 252 | 252.5 | 129.7 |
小亮 | 255 | m | 88.7 |
根据以上信息,回答下列问题:
(1)m= ;
(2)历届比赛表明:成绩达到266cm就有可能夺冠,成绩达到270cm就能打破纪录(积分加倍),根据这6次选拔赛成绩,你认为应选 (填“小明”或“小亮”)参加这项比赛,理由是 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(s),y=PC2,则y关于x的函数的图像大致为 ( )
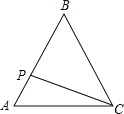
A. 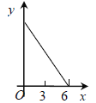 B.
B. 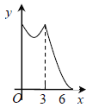 C.
C. 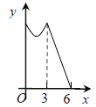 D.
D. 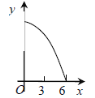
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC、AO于点M、N,再分别以M、N为圆心,大于![]() MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
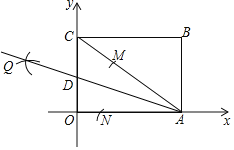
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某户外看台的截面图,长10m的看台AB与水平地面AP的夹角为35°,与AP平行的平台BC长为1.9m,点F是遮阳棚DE上端E正下方在地面上的一点,测得AF=2m,在挡风墙CD的点D处测得点E的仰角为26°,求遮阳棚DE的长. (参考数据:sin35°≈0.57,cos35°≈0.82, sin26°≈0.44,cos26°≈0.90)
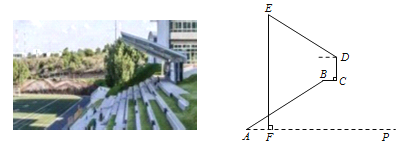
查看答案和解析>>
科目:初中数学 来源: 题型:
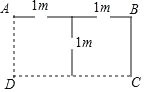
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com