Question

20．如图，足够大的直角三角板ABP的顶点P固定在直线OM：y=x上，且点P的横坐标为$\sqrt{3}$，直角三角板的边AP、BP分别与y轴、x轴交于C、D两点，在图1中直角三角板的边AP与y轴垂直．
（1）将图1中的直角三角板绕顶点P逆时针旋转30°，如图2，则PC=2，PD=2；若CD交OP于点E，求△PED的面积；
（2）将（1）问中的三角板继续绕顶点P逆时针旋转，若PA交直线OD于点G，当△PGD与△OCD相似时，求OD的长．

Answer 1

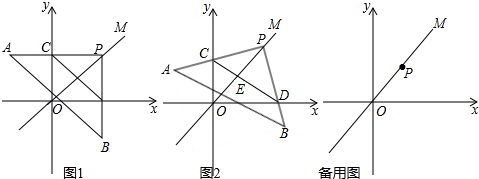
分析 （1）如图1所示：过点P作PF⊥y轴，垂足为FPG⊥x轴，垂足为G．先求得点P的坐标为（$\sqrt{3}$，$\sqrt{3}$），然后由特殊锐角三角函数值可求得PC=2，PD=2，FC=GD=1，于是得到C（0，$\sqrt{3}-1$），D（$\sqrt{3}+1$，0），由角平分线的性质可知点E到x轴、y轴的距离相等，故此$\frac{{S}_{△COE}}{{S}_{△DOE}}=\frac{OC}{OD}=\frac{EC}{ED}$，从而可求得$\frac{ED}{DC}=\frac{\sqrt{3}+1}{2\sqrt{3}}$，最后根据${S}_{PED}=\frac{\sqrt{3}+1}{2\sqrt{3}}×{S}_{△PDC}$求解即可；
（2）设直线PA的解析式为y=k（x-$\sqrt{3}$）+$\sqrt{3}$，直线PB的解析式为y₁=$-\frac{1}{k}$（x-$\sqrt{3}$）+$\sqrt{3}$，可求得G（$-\frac{\sqrt{3}}{k}+\sqrt{3}$，0），点C（0，$-\sqrt{3}k+\sqrt{3}$）点D的坐标为（$\sqrt{3}k+\sqrt{3}$，0），如图2、图3所示利用相似三角形的性质可求得k的值，从而可求得OD的长．

解答 解：（1）如图1所示：过点P作PF⊥y轴，垂足为F，过点P作PG⊥x轴，垂足为G．

∵点P的横坐标为$\sqrt{3}$且点P在y=x上，
∴点P的坐标为（$\sqrt{3}$，$\sqrt{3}$）．
∴PF=PG=$\sqrt{3}$．
∵∠FPC=∠DPG=30°，
∴PC=$\frac{PF}{\frac{\sqrt{3}}{2}}$=2，PD=$\frac{PF}{\frac{\sqrt{3}}{2}}$=2．
∴FC=GD=1．
∴点C的坐标为（0，$\sqrt{3}-1$），点D的坐标为（$\sqrt{3}+1$，0）．
∵点E在y=x上，
∴点E到x轴、y轴的距离相等．
∴$\frac{{S}_{△COE}}{{S}_{△DOE}}=\frac{OC}{OD}=\frac{EC}{ED}$，即$\frac{CE}{ED}=\frac{\sqrt{3}-1}{\sqrt{3}+1}$．
∴$\frac{ED}{DC}=\frac{\sqrt{3}+1}{2\sqrt{3}}$．
∴${S}_{△PED}=\frac{\sqrt{3}+1}{2\sqrt{3}}×{S}_{△PDC}$=$\frac{\sqrt{3}+1}{2\sqrt{3}}×\frac{1}{2}×2×2$=$\frac{3+\sqrt{3}}{3}$．
故答案为：2；2．
（2）设直线PA的解析式为y=k（x-$\sqrt{3}$）+$\sqrt{3}$，直线PB的解析式为y₁=$-\frac{1}{k}$（x-$\sqrt{3}$）+$\sqrt{3}$．
令y=0得：k（x-$\sqrt{3}$）+$\sqrt{3}$=0，解得：x=$-\frac{\sqrt{3}}{k}$+$\sqrt{3}$，令x=0得；y=-$\sqrt{3}k+\sqrt{3}$，
则点G的坐标为（$-\frac{\sqrt{3}}{k}+\sqrt{3}$，0），点C的坐标为（0，$-\sqrt{3}k+\sqrt{3}$）．
令y₁=0得$-\frac{1}{k}$（x-$\sqrt{3}$）+$\sqrt{3}$=0，解得：x=$\sqrt{3}$k+$\sqrt{3}$．
∴点D的坐标为（$\sqrt{3}k+\sqrt{3}$，0）．
如图2所示：

∵△PDG∽△DOC，
∴∠PGD=∠CDG．
∴CG=CD．
∵OC⊥GD，
∴OG=OD．
∴$-\frac{\sqrt{3}}{k}+\sqrt{3}$+$\sqrt{3}k+\sqrt{3}$=0．
解得：k₁=$\sqrt{2}-1$，k₂=$-\sqrt{2}-1$（舍去）．
∴OD=$\sqrt{3}k+\sqrt{3}$=$\sqrt{6}$．
如图3所示：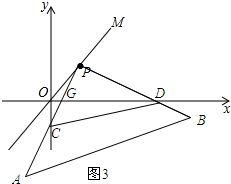

∵△PDG∽△DOC，
∴∠PDG=∠CDO．
∴∠OCG=∠CDO．
∴△OCG∽△ODC．
∴OC²=OG•OD，即$（\sqrt{3}-\sqrt{3}k）^{2}$=（$-\frac{\sqrt{3}}{k}+\sqrt{3}$）×（$\sqrt{3}k+\sqrt{3}$）．
解得：k₁=$\sqrt{2}+1$，k₂=$-\sqrt{2}+1$（舍去），k₃=1（舍去）．
∴OD=$\sqrt{3}k+\sqrt{3}$=$\sqrt{3}×（\sqrt{2}+1）$+$\sqrt{3}$=$\sqrt{6}$+2$\sqrt{3}$．
综上所述，OD的长为$\sqrt{6}$或$\sqrt{6}+2\sqrt{3}$．

点评 本题主要考查的是相似三角形的性质和判定、旋转的性质、一次函数的图象和性质、角平分线的性质，设出直线PA、PB的解析式，求得点C、D、G的坐标（用含k的式子表示），然后由相似三角形的性质求得k的值是解题的关键．