练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

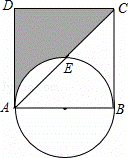
    如图，在边长为4的正方形ABCD中，以AB为直径的半圆与对角线AC交于点E．

    （1）求弧BE所对的圆心角的度数．

    （2）求图中阴影部分的面积（结果保留π）．


     解：（1）连接OE，

    ∵四边形ABCD为正方形，

    ∴∠EAB=45°，

    ∴∠EOB=2∠EAB=90°；

    （2）由（1）∠EOB=90°，

    且AB=4，则OA=2，

    ∴S扇形AOE==π，S△AOE=OA2=2，

    ∴S弓形=S扇形AOE﹣S△AOE=π﹣2，

    又∵S△ACD=AD•CD=×4×4=8，

    ∴S阴影=8﹣（π﹣2）=10﹣π．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


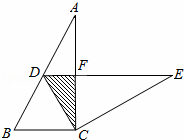
    如图，在Rt△ABC 中，∠ACB=90°，∠A=30°，BC=2．将△ABC绕点C按顺时针方向旋转n度后得到△EDC，此时点D在AB边上，斜边DE交AC边于点F，则n的大小和图中阴影部分的面积分别为（　　）

    　 A． 30，2 B． 60，2 C． 60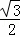， D． 60，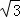

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC面积是45cm2，AB=16cm，AC=14cm，则DE=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，DE∥BC，AD：DB=1：2，BC=2，那么DE=（　　）

    　 A．  B．  C．  D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点P是线段AB的黄金分割点，AP＞PB．若AB=2，则AP=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


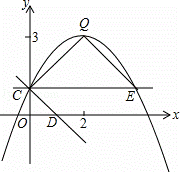
    如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD=OC．

    （1）求直线CD的解析式；

    （2）求抛物线的解析式；

    （3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，求证：△CEQ∽△CDO；

    （4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若不等式组有解，则a的取值范围是（　　）

    　 A． a＞2 B． a＜2 C． a≤2 D． a≥2

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


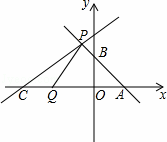
    如图，直线l1：y1=﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2=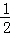x+b过点P．

    （1）求点P坐标和b的值；

    （2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．

    ①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；

    ②求出t为多少时，△APQ的面积小于3；

    ③是否存在t的值，使△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察下列图形它们是按一定规律排列的，依照此规律，第20个图形共有　　　　　　个 ．

    　

    　

     

    查看答案和解析>>

    同步练习册答案