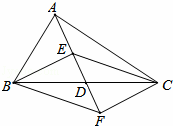
如图，在△ABC中，点D是BC的中点，点E、F分别是线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②BF∥EC；③AB=AC，从中选择一个条件使四边形BECF是菱形，并给出证明，你选择的条件是 （只填写序号）．
科目：初中数学 来源： 题型：
【发现】
如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）
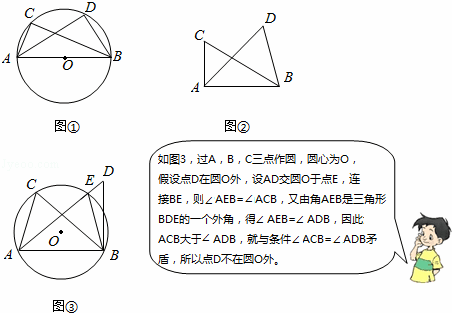
【思考】
如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上吗？
请证明点D也不在⊙O内．
【应用】
利用【发现】和【思考】中的结论解决问题：
若四边形ABCD中，AD∥BC，∠CAD=90°，点E在边AB上，CE⊥DE．
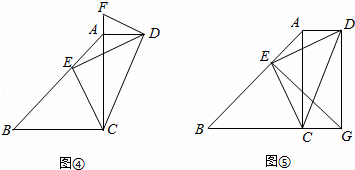
（1）作∠ADF=∠AED，交CA的延长线于点F（如图④），求证：DF为Rt△ACD的外接圆的切线；
（2）如图⑤，点G在BC的延长线上，∠BGE=∠BAC，已知sin∠AED=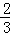
，AD=1，求DG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
某农场急需铵肥8吨，在该农场南北方向分别有一家化肥公司A、B，A公司有铵肥3吨，每吨售价750元；B公司有铵肥7吨，每吨售价700元，汽车每千米的运输费用b（单位：元/千米）与运输重量a（单位：吨）的关系如图所示．
（1）根据图象求出b关于a的函数解析式（包括自变量的取值范围）；
（2）若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m千米，设农场从A公司购买x吨铵肥，购买8吨铵肥的总费用为y元（总费用=购买铵肥费用+运输费用），求出y关于x的函数解析式（m为常数），并向农场建议总费用最低的购买方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱，小刚想知道大家最喜欢哪位“兄弟”，于是在本校随机抽取了一部分学生进行抽查（每人只能选一个自己最喜欢的“兄弟”），将调查结果进行了整理后绘制成如图两幅不完整的统计图，请结合图中提供的信息解答下列问题：
（1）本次被调查的学生有 人．
（2）将两幅统计图补充完整．
（3）若小刚所在学校有2000名学生，请根据图中信息，估计全校喜欢“Angelababy”的人数．
（4）若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动，则两人都是喜欢“李晨”的学生的概率是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
×
+
的运算结果应在哪两个连续自然数之间（ ）
