
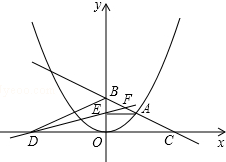
 如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,6),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为a,△BED的面积为S.
如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,6),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为a,△BED的面积为S.分析 (1)由B点坐标可求得BE长,再求得A点坐标,可得AE长,再证明△ABE∽△CBO,可求得CO,结合条件可求得OD,可求得S的值;
(2)分0<a<$\sqrt{6}$和a>$\sqrt{6}$两种情况,可证明△BEA∽△BOD,利用相似三角形的性质可求得BE•DO,可求得S与a的关系式;
(3)①连接AD,根据同高两三角形的面积比为底的比,可得到$\frac{{S}_{△ADF}}{{S}_{△BDF}}$=$\frac{{S}_{△AEF}}{{S}_{△BEF}}$=$\frac{AF}{BF}$=k,再利用面积的和差可得到k=$\frac{{S}_{△ADE}}{{S}_{△BDE}}$,再根据S=2$\sqrt{3}$可求得A点坐标,可求得△ADE的面积,从而可求得k的值,即可得到$\frac{AF}{BF}$;②连接AD,同①的方法可得到k和a的数量关系.
解答 解:
(1)∵点A在二次函数y=x2的图象上,AE⊥y轴于点E且AE=a,
∴点A的坐标为(a,a2),
当a=$\sqrt{3}$时,点A的坐标为($\sqrt{3}$,3),
∵点B的坐标为(0,6),
∴BE=OE=3.
∵AE⊥y轴,
∴AE∥x轴,
∴△ABE∽△CBO,
∴$\frac{AE}{CO}$=$\frac{BE}{BO}$=$\frac{1}{2}$,
∴CO=2$\sqrt{3}$,
∵点D和点C关于y轴对称,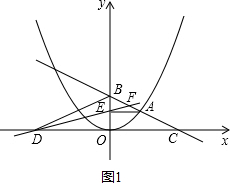
∴DO=CO=2$\sqrt{3}$,
∴S=$\frac{1}{2}$BE•DO=$\frac{1}{2}$×3×2$\sqrt{3}$=3$\sqrt{3}$;
(2)(I)当0<a<$\sqrt{6}$(如图1),
∵点D和点C关于y轴对称,
∴△BOD≌△BOC,
∵△BEA∽△BOC,
∴△BEA∽△BOD,
∴$\frac{BE}{AE}$=$\frac{BO}{DO}$,即BE•DO=AE•BO=6a.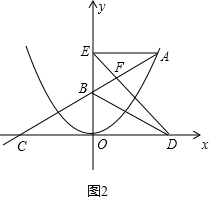
∴S=$\frac{1}{2}$BE•DO=$\frac{1}{2}$×6 a=3a;
(II)当a>$\sqrt{6}$时(如图2),
同(I)解法得:
S=$\frac{1}{2}$BE•DO=$\frac{1}{2}$AE•OB=3a,
由(I)(II)得,S关于a的函数解析式为:S=3a(a>0且a≠$\sqrt{6}$);
(3)①如图3,连接AD,
∵△BED的面积为2$\sqrt{3}$,
∴S=3a=2$\sqrt{3}$,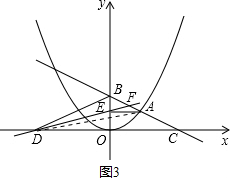
∴点A的坐标为($\frac{2}{3}$$\sqrt{3}$,$\frac{4}{3}$),
∵$\frac{{S}_{△ADF}}{{S}_{△BDF}}$=$\frac{{S}_{△AEF}}{{S}_{△BEF}}$=$\frac{AF}{BF}$=k,
∴S△ADF=k•S△BDF,
S△AEF=k•S△BEF,
∴$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{{S}_{△ADF}-{S}_{△AEF}}{{S}_{△BDF}-{S}_{△BEF}}$=$\frac{k({S}_{△BDF}-{S}_{△BEF})}{{S}_{△BDF}-{S}_{△BEF}}$=k,
∴k=$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{\frac{1}{2}×\frac{2}{3}\sqrt{3}×\frac{4}{3}}{2\sqrt{3}}$=$\frac{2}{9}$,即$\frac{AF}{BF}$=$\frac{2}{9}$;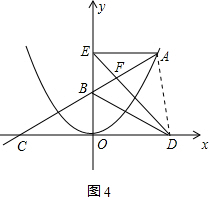
②k与a之间的数量关系为k=$\frac{1}{6}$a2,
如图4,连接AD,
∵$\frac{{S}_{△ADF}}{{S}_{△BDF}}$=$\frac{{S}_{△AEF}}{{S}_{△BEF}}$=$\frac{AF}{BF}$=k,
∴S△ADF=k•S△BDF,S△AEF=k•S△BEF,
∴$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{{S}_{△ADF}+{S}_{△AEF}}{{S}_{△BDF}+{S}_{△BEF}}$=$\frac{k({S}_{△BDF}+{S}_{△BEF})}{{S}_{△BDF}+{S}_{△BEF}}$=k,
∵点A的坐标为(a,a2),S=3a,
∴k=$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{\frac{1}{2}•a•{a}^{2}}{3a}$=$\frac{1}{6}$a2(a>$\sqrt{6}$).
点评 本题主要考查了二次函数的综合应用,涉及了三角形的面积、比例的性质及相似三角形的判定与性质、全等三角形的性质等知识点.解答本题的关键是熟练数形结合思想及转化思想的运用,难度较大.


科目:初中数学 来源: 题型:解答题
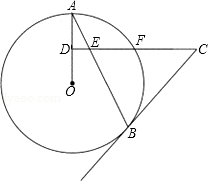 AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
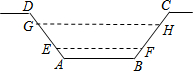 如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )| A. | 0.55 | B. | 0.8 | C. | 0.6 | D. | 0.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
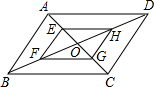 如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.
如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com