练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲、乙两地相距135千米，大小两辆汽车从甲地开往乙地，大汽车比小汽车早出发4小时，小汽车比大汽车早到30分钟，小汽车和大汽车的速度之比为5∶2，求两车的速度．

    【答案】解：设小汽车的速度为5x千米/时，则大汽车的速度为2x千米/时，列方程得： ，解得 ，经检验， 是原方程的解，且符合题意，所以 ， ，所以小汽车的速度为45千米/时，则大汽车的速度为18千米/时
    【解析】根据已知条件小汽车和大汽车的速度之比为5∶2，可设小汽车的速度为5x千米/时，则大汽车的速度为2x千米/时，相等关系是小汽车走135千米所用的时间=大汽车走135千米所用的时间-先走的4小时-晚到的半小时，根据相等关系列方程，解这个分式方程，并检验即可求解。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，不经过原点的直线与双曲线y=相交于点A（m，2），B（n，﹣1），其中m＞0，n＜0．

    （1）求m与n之间的数量关系；

    （2）若OA=OB，求该双曲线和直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a﹣3是a2+5a+m的一个因式，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图①，在平面直角坐标系xOy中，A（0，5），C（，0），AOCD为矩形，AE垂直于对角线OD于E，点F是点E关于y轴的对称点，连AF、OF．

    （1）求AF和OF的长；

    （2）如图②，将△OAF绕点O顺时针旋转一个角α（0°＜α＜180°），记旋转中的△OAF为△OA′F′，在旋转过程中，设A′F′所在的直线与线段AD交于点P，与线段OD交于点Q，是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时点P坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了普及环保知识，增强环保意识，某中学组织了环保知识竞赛活动，初中三个年级根据初赛成绩分别选出了10名同学参加决赛（满分为100分）如表所示：
    决赛成绩（单位：分）

    （1）请你填写下表：

    平均数

    众数

    中位数

    七年级

    85.5

    87

    八年级

    85.5

    85

    九年级

    84


    （2）请从以下两个不同的角度对三个年级的决赛成绩进行分析：
    从平均数和众数相结合看（分析哪个年级成绩好些）：；
    从平均数和中位数相结合看（分析哪个年级成绩好些）：；
    （3）如果在每个年级参加决赛的选手中分别选出三人参加决赛，你认为哪个年级的实力更强一些。说明理由：。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中，对角线相交于点O；E、F、G、H分别是AD、BD、 BC、AC的中点．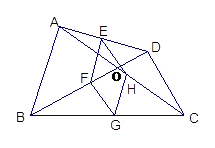

    （1）说明四边形EFGH是平行四边形；
    （2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，对于平面内任意一点（x，y），若规定以下两种变换：

    ①f（x，y）＝（x+2，y），

    ②g（x，y）＝（﹣x，﹣y），例如按照以上变换有：f（1，1）＝（3，1）；g（f（1，1））＝g（3，1）＝（﹣3，﹣1）．

    则f（g（2，5））＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某乡村在开展“美丽乡村”建设时，决定购买A，B两种树苗对村里的主干道进行绿化改造，已知购买A种树苗3棵，B种树苗4棵，需要380元；购买A种树苗5棵，B种树苗2棵，需要400元．

    （1）求购买A，B两种树苗每棵各需多少元？

    （2）现需购买这两种树苗共100棵，要求购买A种树苗不少于60棵，且用于购买这两种树苗的资金不超过5620元．则有哪几种购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，对角线、交于点，将沿直线翻折，点落在点处，且，连接．求证：

    （）是等边三角形．

    （）．

    查看答案和解析>>

    同步练习册答案