
分析 (1)根据抛物线过C点,可得出c=-3,对称轴x=1,则-$\frac{b}{2a}$=1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.
(2)根据圆和抛物线的对称性可知:圆心必在对称轴上.因此可用半径r表示出M、N的坐标,然后代入抛物线中即可求出r的值.
解答  解:(1)将C(0,-3)代入y=ax2+bx+c,
解:(1)将C(0,-3)代入y=ax2+bx+c,
得c=-3.
将c=-3,B(3,0)代入y=ax2+bx+c,
得9a+3b+c=0.(1)
∵直线x=1是对称轴,
∴-$\frac{b}{2a}$=1(2)
将(2)代入(1)得
a=1,b=-2.
所以,二次函数得解析式是y=x2-2x-3.
(2)设M(x1,y)、N(x2,y),所求圆的半径为r,
则x2-x1=2r,①
∵对称轴为直线x=1,即$\frac{{x}_{1}+{x}_{2}}{2}$=1,
∴x2+x1=2,②
由①、②得:x2=r+1,③
将N(r+1,y)代入解析式y=x2-2x-3,
得y=(r+1)2-2(r+1)-3,
整理得:y=r2-4,
由所求圆与x轴相切,得到r=|y|,即r=±y,
当y>0时,r2-r-4=0,
解得,r1=$\frac{1+\sqrt{17}}{2}$,r2=$\frac{1-\sqrt{17}}{2}$(舍去),
当y<0时,r2+r-4=0,
解得,r1=$\frac{-1+\sqrt{17}}{2}$,r2=$\frac{-1-\sqrt{17}}{2}$(舍去).
所以圆的半径是$\frac{1+\sqrt{17}}{2}$或$\frac{-1+\sqrt{17}}{2}$.
点评 本题考查了待定系数法求二次函数解析式、切线的性质、轴对称图形等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法,正确的画出图形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
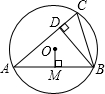 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A. | OM的长 | B. | $\frac{1}{2}$OM的长 | C. | 2OM的长 | D. | CD的长 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
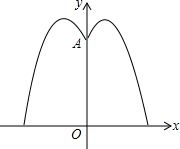 某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子0A,0恰在水面中心,安装在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过0A的任意平面上,抛物线形状如图所示,建立平面直角坐标系,右边-条抛物线水流喷出的高度y(m)与水面距离x(m)之间的关系式是y=-x2+2x+$\frac{7}{2}$.请回答下列问题:
某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子0A,0恰在水面中心,安装在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过0A的任意平面上,抛物线形状如图所示,建立平面直角坐标系,右边-条抛物线水流喷出的高度y(m)与水面距离x(m)之间的关系式是y=-x2+2x+$\frac{7}{2}$.请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com