

分析 (1)根据顶点坐标,可得顶点式解析式,根据待定系数法,可得答案;
(2)根据切线的性质,可得CE与CA的关系,根据直角三角形的性质,可得∠EDC的度数,根据正切函数,可得答案;
(3)根据解方程组,可得P点坐标,根据三角形的面积间的关系,可得关于k的方程,根据解方程,可得答案.
解答 解:(1)由抛物线的顶点为(0,4),
可设抛物线解析式为y=ax2+4.
由抛物线过点(2,0),得
0=4a+4,解得a=-1,
∴抛物线解析式为y=-x2+4;
(2)①如图,连接CE,CD.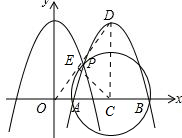
∵OD是⊙C的切线,
∴CE⊥OD.
在Rt△CDE中,∠CED=90°,CE=AC=2,DC=4,
∴∠EDC=30°.
∴在Rt△CDO中,∠OCD=90°,CD=4,∠ODC=30°,
∴OC=CDtan30°=$\frac{4\sqrt{3}}{3}$,
∴当直线OD与以AB为直径的圆相切时,k=OC=$\frac{4\sqrt{3}}{3}$;
②平移k个单位后的抛物线的解析式是y=(x-k)2+4
它与y=x2+4交于点P,可得点P的坐标是($\frac{k}{2}$,-$\frac{{k}^{2}}{4}$+4),
∴当k<4时,S△ABP=$\frac{1}{2}$AB•yP=$\frac{1}{2}$×4(4-$\frac{{k}_{2}}{4}$)=8-$\frac{{k}^{2}}{2}$;
当k>4时,S△ABP=$\frac{1}{2}$AB•yP=$\frac{1}{2}$×4($\frac{{k}^{2}}{4}$-4)=$\frac{{k}^{2}}{2}$-8
又∵S△ABD=$\frac{1}{2}$AB•D=$\frac{1}{2}$×4×4=8,
∴$8-\frac{k^2}{2}=4$或$\frac{k^2}{2}-8=4$,解得k=2$\sqrt{2}$或k=2$\sqrt{6}$.
点评 本题考查了二次函数综合题,(1)利用待定系数法求函数解析式;(2)利用切线的性质得出CE的长,利用直角三角形的性质得出∠EDC的度数,又利用了正切函数;(3)利用三角形面积间的关系得出关于k的方程是解题关键,注意要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:解答题
 已知抛物线y=x2-2x-3.
已知抛物线y=x2-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
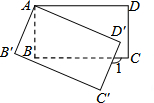 如图,将矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′的位置,旋转角为α(0<α<90°),若∠1=110°,则∠α=( )
如图,将矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′的位置,旋转角为α(0<α<90°),若∠1=110°,则∠α=( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
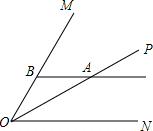 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com