
分析 (1)先进行二次根式的化简,然后进行乘法运算;
(2)根据二次根式的乘法发展和除法法则求解;
(3)先进行二次根式的化简,然后合并;
(4)先进行二次根式的化简,然后合并;
(5)根据二次根式的乘法法则求解;
(6)先进行二次根式的化简,然后合并.
解答 解:(1)原式=15$\sqrt{3}$×$\sqrt{6}$
=45$\sqrt{2}$;
(2)原式=50a2b÷15$\sqrt{\frac{a}{b}}$
=$\frac{10}{3}$a2$\sqrt{ab}$;
(3)原式=2$\sqrt{x}$+3$\sqrt{x}$-2$\sqrt{x}$
=3$\sqrt{x}$;
(4)原式=$\frac{2\sqrt{3}(2\sqrt{3}+3)}{3}$-3-2$\sqrt{3}$
=4+2$\sqrt{3}$-3-2$\sqrt{3}$
=1;
(5)原式=25$\sqrt{2}$-10$\sqrt{3}$+10$\sqrt{3}$-6$\sqrt{2}$
=19$\sqrt{2}$;
(6)原式=$\frac{ab+(a-b)\sqrt{ab}-ab}{b(a-b)}$+$\frac{ab+(a-b)\sqrt{ab}-ab}{a(a-b)}$
=$\frac{\sqrt{ab}}{b}$+$\frac{\sqrt{ab}}{a}$
=$\frac{\sqrt{ab}(b-a)}{ab}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及二次根式的合并.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
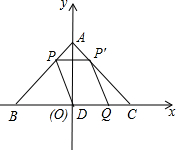 在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.
在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com