
【题目】如图,在平面直角坐标系中,已知OA=12cm,OB=6cm.点P从点O开始沿0A边向点A以1cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间(0≤t<6),那么:
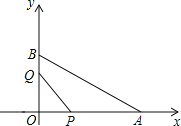
(1)设ΔPOQ的面积为y,求y关于t的函数关系式;
(2)当ΔPOQ的面积为4.5cm时,ΔPOQ沿直线PQ翻折后得到ΔPCQ.试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.
【答案】(1)![]() ;(2)点C不在直线AB上;(3)t=2或t=4
;(2)点C不在直线AB上;(3)t=2或t=4
【解析】
(1)根据S△POQ= ![]() POOQ,再把OQ=6-t,OP=t代入整理即可;
POOQ,再把OQ=6-t,OP=t代入整理即可;
(2)令![]() ,求出t,即可求出OP=3,OQ=3,即可知△POQ是等腰直角三角形,根据折叠的性质知点C的坐标是(3,3),求出直线AB的函数关系式,把点C代入函数解析式即可得出点C不在直线AB上;
,求出t,即可求出OP=3,OQ=3,即可知△POQ是等腰直角三角形,根据折叠的性质知点C的坐标是(3,3),求出直线AB的函数关系式,把点C代入函数解析式即可得出点C不在直线AB上;
(3)分两种情形讨论即可①若△POQ∽△AOB时,得 ![]() ,②若△POQ∽△BOA时,得
,②若△POQ∽△BOA时,得 ![]() ,分别解方程即可.
,分别解方程即可.
(1)∵OQ=6-t
∴![]()
(2)当△POQ的面积为4.5cm时,即![]()
∴t=3
易得△POQ是等腰直角三角形
∴点C的坐标是(3,3)
而直线AB的函数关系式是![]()
当![]() 时,
时,![]()
∴点C不在直线AB上
(3)∵OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,
∴OQ=(6-t)cm,
∵点Q从点B开始沿BO边向点O以1cm/s的速度移动,
∴OP=t(cm),
若△POQ∽△AOB时,
得 ![]() 即
即![]()
整理得:12-2t=t,
解得:t=4,
则当t=4时,△POQ与△AOB相似;
若△POQ∽△BOA时,
得 ![]() ,
,
即![]()
解得:t=2,
则当t=2时,△POQ与△BOA相似;
综上所述:当t=4s或2s时,△POQ与△AOB相似.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,
内部,![]() 时,
时,![]() ________.
________.
(2)当圆心![]() 在
在![]() 内部,四边形
内部,四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的度数;
的度数;
(3)当圆心![]() 在
在![]() 外部,四边形
外部,四边形![]() 为平行四边形时,请直接写出
为平行四边形时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
添项法是代数变形中非常重要的一种方法,在整式运算和因式分解中使用添项法往往会起到意想不到的作用,例如:
例1:计算(3+1)(32+1)(34+1)(38+1)(316+1)(332+1)
解:原式=![]() (3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)(332+1)
(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)(332+1)
=![]() (32﹣1)(32+1)(34+1)(38+1)(316+1)(332+1)
(32﹣1)(32+1)(34+1)(38+1)(316+1)(332+1)
=![]() (34﹣1)(34+1)(38+1)(316+1)(332+1)
(34﹣1)(34+1)(38+1)(316+1)(332+1)
……
=![]()
例2:因式分解:x4+x2+1
解:原式=x4+x2+1=x4+2x2+1﹣x2
=(x2+1)2﹣x2
=(x2+1+x)(x2+1﹣x)
根据材料解决下列问题:
(1)计算:![]() ;
;
(2)小明在作业中遇到了这样一个问题,计算![]() ,通过思考,他发现计算式中的式子可以用代数式之x4+4来表示,所以他决定先对x4+4先进行因式分解,最后果然发现了规律;轻松解决了这个计算问题.请你根据小明的思路解答下列问题:
,通过思考,他发现计算式中的式子可以用代数式之x4+4来表示,所以他决定先对x4+4先进行因式分解,最后果然发现了规律;轻松解决了这个计算问题.请你根据小明的思路解答下列问题:
①分解因式:x4+4;
②计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
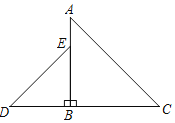
【题目】如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=![]() .将△BDE绕点B逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.
.将△BDE绕点B逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
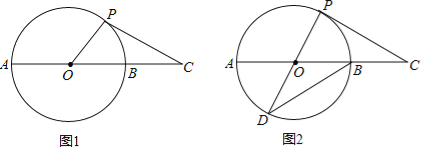
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销的太阳路灯,标价为4000元/个,促销活动期间,其优惠方法如下:
A.一次性购买数量不超过80个,按标价收费;
B.一次性购买数量超过80个,每多买一个,所购路灯每个可降价8元,但单价最低不能低于3200元/个.
(1)购买80个这样的路灯,应需付款_________________元.
(2)若一顾客一次性购买这样的路灯用去516000元,则该顾客实际购买了多少个这样的路灯.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON,点A在射线OM上.根据下列方法画图.
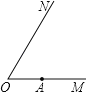
①以O为圆心,OA长为半径画圆,交ON于点B,交射线OM的反向延长线于点C,连接BC;
②以OA为边,在∠MON的内部,画∠AOP=∠OCB;
③连接AB,交OP于点E;
④过点A作⊙O的切线,交OP于点F.
(1)依题意补全图形;
(2)求证∠MOP=∠PON;
(3)若∠MON=60°,OF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=![]() .其中正确的是( )
.其中正确的是( )

A. ①②③④ B. ①② C. ①③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则下列结论:①4ac-b2<0;②2a-b=0;③a+b+c<0;④点(x1,y1),(x2,y2)在抛物线上,若x1<x2,则y1<y2 .正确结论的个数是( )
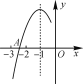
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com