
【题目】某家具厂生产一种课桌和椅子,课桌每张定价180元,椅子每把定价80元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张课桌就赠送一把椅子
方案二:课桌和椅子都按定价的80%付款
某校计划添置100张课桌和![]() 把椅子,
把椅子,
(1)若![]() ,请计算哪种方案划算;
,请计算哪种方案划算;
(2)若![]() ,请用含
,请用含![]() 的代数式分别把两种方案的费用表示出来
的代数式分别把两种方案的费用表示出来
(3)若![]() ,乔亚萍认为用方案一购买省钱,小兰认为用方案二购买省钱,如果两种方案可以同时使用,你能帮助学校设计一种比乔亚萍和小兰的方案都更省钱的方案吗?若能,请你写出方案,若不能,请说明理由.
,乔亚萍认为用方案一购买省钱,小兰认为用方案二购买省钱,如果两种方案可以同时使用,你能帮助学校设计一种比乔亚萍和小兰的方案都更省钱的方案吗?若能,请你写出方案,若不能,请说明理由.
【答案】(1)方案一划算;(2)方案一:(80x+10000),方案二:(64x+14400);(3)先按方案一购买100张桌子,同时送100把椅子;再按方案二购买220把椅子最省.
【解析】
(1)当x=100时,根据各自的优惠方案,分别求出两种方案的钱数,比较即可;
(2)当x>100时,分别表示出两种方案的钱数即可;
(3)方案设计问题,可以两个方案结合在一起使用,
解:(1)当x=100时,
方案一:100×180=18000(元);
方案二:100×(180+80)×80%=20800(元),
∵18000<20800,
∴方案一划算;
(2)当x>100时,
方案一:100×180+80(x-100)=80x+10000;
方案二:(100×180+80x)×80%=64x+14400,
答:方案一、方案二的费用为:(80x+10000)、(64x+14400)元;
(3)当x=320时,
方案一:100×180+80×(320-100)=35600(元);
方案二:(100×180+80×320)×80%=34880(元);
方案三:先按方案一购买100张课桌,同时送100把椅子;再按方案二购买220把椅子,
100×180+80×220×80%=32080(元),
35600>34880>32080,
则先按方案一购买100张桌子,同时送100把椅子;再按方案二购买220把椅子最省.


科目:初中数学 来源: 题型:
【题目】小华间学早晨跑步,他从自己家出发.先向东跑了2km则达小盛家,又继续向东跑了1.5km到这小昌家,然后又向西跑到学校.如果小华跑步的速度是均匀的,且到达小盛家用了8分钟,整个跑步过程共用时32分钟,以小华家为原点,向东为正方向,用1个单位长度表示1km,建立数轴.
(1)依题意画出数轴,分别用点A表示出小盛家、用点B表示出小昌家;
(2)在数轴上,用点C表示出学校的位置;
(3)求小盛家与学校之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
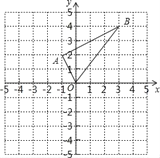
【题目】如图在平面直角坐标系中,已知点A(﹣1,2),B(3,4).
(1)画出△ABO向上平移2个单位,再向左平移4个单位后所得的图形△A′B′O′;
(2)写出A、B、O后的对应点A′、B′、O′的坐标;
(3)求两次平移过程中OB共扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装厂现有甲种布料38米,乙种布料26米,现计划用这两种布料生产L.M两种型号的童装共50套.已知做一套L.M型号的童装所需用布料和所获得利润如下表:
甲种布料 | 乙种布料 | 获 利 | |
L型 | 0.5米 | 1米 | 45元 |
M型 | 0.9米 | 0.2米 | 30元 |
假设L型号的服装生产![]() 套,请你写出满足题意的不等式组,求出其解集;并根据计算结果,设计生产方案.
套,请你写出满足题意的不等式组,求出其解集;并根据计算结果,设计生产方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
小红的作法如下:
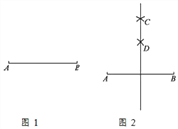
如图,①分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于点C;
AB的长为半径作弧,两弧相交于点C;
②再分别以点A和点B为圆心,大于![]() AB的长为半径(不同于①中的半径)作弧,两弧相交于点D,使点D与点C在直线AB的同侧;
AB的长为半径(不同于①中的半径)作弧,两弧相交于点D,使点D与点C在直线AB的同侧;
③作直线CD.
所以直线CD就是所求作的垂直平分线.
老师说:“小红的作法正确.”
请回答:小红的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
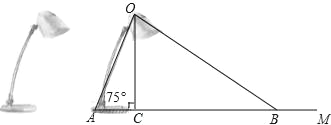
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
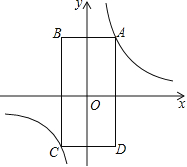
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点重合,在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数![]() 中,k的值的变化情况是( )
中,k的值的变化情况是( )
A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com