
【题目】设O是等边三角形ABC内一点,已知∠AOB=130°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
A.65° B.60° C.45° D.70°
【答案】B
【解析】
试题分析:以B为中心,将△BOA逆时针方向旋转60°,则点A落在点C上,点O落在点D上,连接OD,找出△COD即为以线段OA,OB,OC为边构成的三角形,再由角与角之间的关系即可得出结论.
解:以B为中心,将△BOA逆时针方向旋转60°,则点A落在点C上,点O落在点D上,连接OD,如图所示.
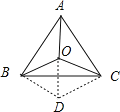
∵OB=BD,∠OBD=60°,
∴△BOD是等边三角形,
∴OD=OB,
又∵CD=OA,
故△COD是以OA,OB,OC为边构成的一个三角形.
∵∠BOC=125°,∠BOD=60°,
∴∠COD=65°;
又∵∠BDC=∠AOB=130°,∠BDO=60°,
∴∠ODC=70°;
从而∠OCD=180°﹣65°﹣70°=45°.
故求得以线段OA,OB,OC为边构成的三角形的各角为65°,70°,45°.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美国航空航天局发布消息,2011年3月19日,月球将到达19年来距离地球最近的位置,它与地球的距离约为356000千米,其中356000用科学记数法表示为 ( )
A. 3.56×105 B. 0.356×106 C. 3.56×104 D. 35.6×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了每个营业员在某月的销售额,统计图如下,根据统计图中给出的信息,解答下列问题:
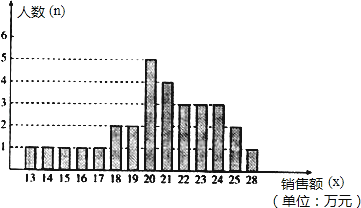
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.称职和优秀的营业员共有多少人?所占百分比是多少?
(2)根据(1)中规定,所有称职以上(职称和优秀)的营业员月销售额的中位数、众数和平均数分别是多少?
(3)为了调动营业员的工作积极性,决定制定月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得称职以上(称职和优秀)的营业员有一半能获奖,你认为这个奖励标准应定月销售额为多少元合适?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个完全相同的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为___________s

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.

(1)求证:四边形ADEF是平行四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形,并说明理由.
(3)当△ABC满足什么条件时,边形ADEF是菱形,并说明理由.
(4)当△ABC满足什么条件时,四边形ADEF是正方形,不要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com