
 ��ͼ��ƽ��ֱ������ϵ�У���A��B��C��x���ϣ���D��E��y���ϣ�OA=OD=2��OC=OE=4��BΪ�߶�OA���е㣮ֱ��AD�뾭��B��E��C����������߽���F��G���㣬����Գ��ύ��M����PΪ�߶�FG��һ�����㣨��F��G���غϣ���PQ��y���������߽��ڵ�Q��
��ͼ��ƽ��ֱ������ϵ�У���A��B��C��x���ϣ���D��E��y���ϣ�OA=OD=2��OC=OE=4��BΪ�߶�OA���е㣮ֱ��AD�뾭��B��E��C����������߽���F��G���㣬����Գ��ύ��M����PΪ�߶�FG��һ�����㣨��F��G���غϣ���PQ��y���������߽��ڵ�Q������ ��1�����������B��C��E�����꣬�����������߽���ʽΪy=ax2+bx+c���г�a��b��c����Ԫһ�η����飬���a��b��c��ֵ���ɣ�
��2�����ù��ɶ������涨�����������CBD��ֱ�������Σ���OP=OC��PC=OC��PC=PO���ֽ��н������ۼ��ɣ�
��3���������MN��ֵ������x��ʾ��PQ�ij����������ε����ʼ����г�x��һԪ���η��̣����x��ֵ�����������жϣ�
��� �⣺��1����OA=OD=2��BΪ�߶�OA���е㣬
��OB=1��
���B������-1��4����
��OC=OE=4��
���E��0��4������C��4��0����
�������߽���ʽΪy=ax2+bx+c��
��$\left\{\begin{array}{l}{a-b+c=0}\\{c=4}\\{16a+4b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-1}\\{b=3}\\{c=4}\end{array}\right.$��
�������߽���ʽΪy=-x2+3x+4��
��2����BDC��ֱ�������Σ�
��BD2=BO2+DO2=5��CD2=DO2+CO2=20��BC2=��BO+CO��2=25��
��BD2+CD2=BC2��
���BDC��ֱ�������Σ�
�ߵ�A�����ǣ�-2��0������D�����ǣ�0��2����
��ֱ��AD�Ľ���ʽΪy=x+2��
���P������x��x+2����
��OP=OCʱ��x2+��x+2��2=16��
���x=1+$\sqrt{7}$��x=1-$\sqrt{7}$�����������⣬��ȥ����
��ʱ��P��1+$\sqrt{7}$��3+$\sqrt{7}$����
��PC=OCʱ����x+2��2+��4-x��2=16�������⣻
��PO=PCʱ����P��OC���д����ϣ�
���P�ĺ�������2����P��������Ϊ4����ʱ��P����Ϊ��2��4����
���ϣ�����POC�ǵ���������ʱ����P������Ϊ��1+$\sqrt{7}$��3+$\sqrt{7}$����2��4����
��3����y=-x2+3x+4=-��x-$\frac{3}{2}$��2+$\frac{25}{4}$��
���N�����ǣ�$\frac{3}{2}$��$\frac{25}{4}$����
�ߵ�M��ֱ��AC�ϣ�
���M������$\frac{3}{2}$��$\frac{7}{2}$����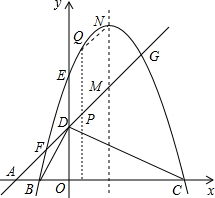
��MN=$\frac{11}{4}$��
���P��x��x+2����Q��x��-x2+3x+4������PQ=-x2+2x+2��
��PQMN��������PQ=MN��
��$\frac{11}{4}$=-x2+2x+2��
���x1=0.5��x2=1.5��
��x2=1.5ʱ����P���M�غϣ�
��x1=0.5ʱ�����PM=$\sqrt{2}$���������β����ڣ�
���� ������Ҫ�����˶��κ����ۺ��⣬�����漰������ϵ���������������ʽ�����������ε����ʡ����ε��ж������ʵ�֪ʶ������⣨2���ʵĹؼ��ǶԵ��������ν��з������ۣ����3���ʵĹؼ������MN�ij��Լ���x��ʾPQ�ij���������һ�����Ѷȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b2-4ac��0 | B�� | b2-4ac��0 | C�� | b2-4ac��0 | D�� | b2-4ac��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 17�ˣ�k=8 | B�� | 17�ˣ�k=9 | C�� | 11�ˣ�k=10 | D�� | 11�ˣ�k=8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
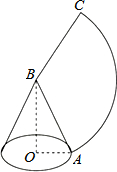 ��ͼ����Rt��AOB��ֱ�DZ�OB���ڵ�ֱ����תһ�ܣ��õ�����ת��IJ���չ��ͼ��Բ�ĽǶ���Ϊ120�㣬��OB=4$\sqrt{2}$cm�������ת��ı����Ϊ��������
��ͼ����Rt��AOB��ֱ�DZ�OB���ڵ�ֱ����תһ�ܣ��õ�����ת��IJ���չ��ͼ��Բ�ĽǶ���Ϊ120�㣬��OB=4$\sqrt{2}$cm�������ת��ı����Ϊ��������| A�� | 16��cm2 | B�� | 12��cm2 | C�� | 18��cm2 | D�� | 12$\sqrt{2}$��cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
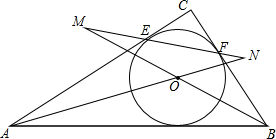 ��Rt��ABC�У���C=90�㣬��������Բ��O�ֱ����AC��BC�����ڵ�E��F������BO��A0��ֱ��EF�ڵ�M��N����֤��$\frac{1}{5}$��$\frac{{S}_{��OMN}}{{S}_{��ABC}}$��$\frac{1}{4}$��
��Rt��ABC�У���C=90�㣬��������Բ��O�ֱ����AC��BC�����ڵ�E��F������BO��A0��ֱ��EF�ڵ�M��N����֤��$\frac{1}{5}$��$\frac{{S}_{��OMN}}{{S}_{��ABC}}$��$\frac{1}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ������ | B�� | �Խ����ഹֱ��ƽ�� | ||
| C�� | �����߶���� | D�� | �Խ���ƽ��һ��Խ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com