Question

7．已知如图，⊙P与x轴切于点O，P点的坐标为（0，2），点A在⊙P上，且A点的坐标为（1，2+$\sqrt{3}$），⊙P沿x轴正方向滚动，当点A第一次落在x轴上时，点P的坐标为（$\frac{5}{3}π$，2）（结果保留π）

Answer 1

分析 过点A，作AB⊥y轴于点B，AC⊥x轴于点C，由点A的坐标，可求出∠APB的度数，进而可得到∠APO的度数，再根据点P的横坐标是A转过的长度，纵坐标是2，由弧长公式即可求解．

解答 解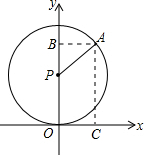：过点A，作AB⊥y轴于点B，AC⊥x轴于点C，易得四边形ABOC是矩形，
∴AC=BO，AB=OC，
∵A点的坐标为（1，2+$\sqrt{3}$），⊙P的半径是2，
∴AB=OC=1，BP=AC-OP=2+$\sqrt{3}$-2=$\sqrt{3}$，
∴tan∠APB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$
∴∠APB=30°，
∴∠APO=150°，
∴A转过的长度=$\frac{150×π×2}{180}$=$\frac{5}{3}π$，
即点P的坐标是（$\frac{5}{3}π$，2）．
故答案为（$\frac{5}{3}π$，2）．

点评 本题主要考查了切线的性质，坐标与图形的关系，弧长公式的计算，掌握公式是解题的关键．