
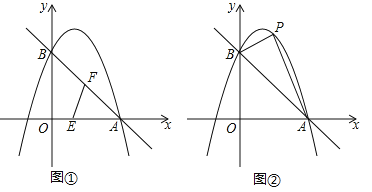
【题目】如图,已知抛物线![]() 经过A(3,0),B(0,3)两点.
经过A(3,0),B(0,3)两点.
(1)求此抛物线的解析式和直线AB的解析式;
(2)如图①,动点E从O点出发,沿着OA方向以1个单位/秒的速度向终点A匀速运动,同时,动点F从A点出发,沿着AB方向以![]() 个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.
【答案】(1)![]() ,y=﹣x+3;(2)
,y=﹣x+3;(2)![]() ;(3)存在面积最大,最大是
;(3)存在面积最大,最大是![]() ,此时点P(
,此时点P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)用待定系数法求出抛物线,直线解析式;
(2)分两种情况进行计算即可;
(3)确定出面积达到最大时,直线PC和抛物线相交于唯一点,从而确定出直线PC解析式,根据锐角三角函数求出BD,计算即可.
试题解析:(1)∵抛物线![]() 经过A(3,0),B(0,3)两点,∴
经过A(3,0),B(0,3)两点,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,设直线AB的解析式为y=kx+n,∴
,设直线AB的解析式为y=kx+n,∴![]() ,∴
,∴![]() ,∴y=﹣x+3;
,∴y=﹣x+3;
(2)由运动得,OE=t,AF=![]() t,∴AE=OA﹣OE=3﹣t,∵△AEF为直角三角形,∴①△AOB∽△AEF,∴
t,∴AE=OA﹣OE=3﹣t,∵△AEF为直角三角形,∴①△AOB∽△AEF,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() ,②△AOB∽△AFE,∴
,②△AOB∽△AFE,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() ;
;
(3)如图,存在,过点P作PC∥AB交y轴于C,∵直线AB解析式为y=﹣x+3,∴设直线PC解析式为y=﹣x+b,联立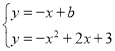 ,∴
,∴![]() ,∴
,∴![]() ,∴△=9﹣4(b﹣3)=0,∴b=
,∴△=9﹣4(b﹣3)=0,∴b=![]() ,∴BC=
,∴BC=![]() ﹣3=
﹣3=![]() ,x=
,x=![]() ,∴ P(
,∴ P(![]() ,
,![]() ).
).
过点B作BD⊥PC,∴直线BD解析式为y=x+3,∴![]() BD=
BD=![]() ,∴BD=
,∴BD=![]() ,∵AB=
,∵AB=![]() ,S最大=
,S最大=![]() AB×BD=
AB×BD=![]() =
=![]() .
.
即:存在面积最大,最大是![]() ,此时点P(
,此时点P(![]() ,
,![]() ).
).


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
A.3×106
B.3×105
C.0.3×106
D.30×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是一个严重缺水的国家,大家应加倍珍惜水资源,节约用水,据测试,拧不紧的水龙头每秒钟会滴下 2 滴水,每滴水约 0.05 毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开 4 小时后水龙头滴了约______毫升水(用科学记数法表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店新开张,第一天销售服装a件,第二天比第一天少销售14件,第三天的销售量是第二天的2倍多10件,则这三天销售了( )件.
A. 3a﹣42 B. 3a+42 C. 4a﹣32 D. 3a+32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(2,1),将点A绕原点O旋转180°得到点A′,则点A′的坐标是( )
A.(-1,-2)B.(1,-2)C.(-2,-1)D.(2,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com