
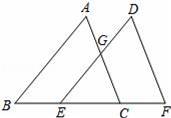
如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.
(1)求证:AB∥DE;
(2)求EG的长.

【考点】全等三角形的判定与性质.
【专题】计算题.
【分析】(1)由BE=CF,利用等式的性质得到BC=EF,利用SSS得到三角形ABC与三角形DEF全等,利用全等三角形对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证;
(2)由BE=CE得到E为BC中点,再由GE与AB平行,利用平行线等分线段定理得到G为AC中点,即GE为中位线,利用中位线定理得到AB=2EG,即可求出EG的长.
【解答】解:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,

 ,
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE;
(2)∵GE∥AB,E为BC中点,
∴G为AC中点,即GE为△ABC中位线,
∴EG=
 AB=5.
AB=5.
【点评】此题考查了全等三角形的判定与性质,以及平行线的判定,熟练掌握全等三角形的判定与性质是解本题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
如图,△DEF与△ABC是位似图形,点O是位似中心,D、E、F分别是OA、OB、OC的中点,则△DEF与△ABC的面积比是( )
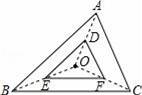

A.1:6 B.1:5 C.1:4 D.1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,∠ACB=90°.经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.
(1)若∠ABC=45°,CD=1(如图),则AE的长为 ;
(2)写出线段AE、CD之间的数量关系,并加以证明;
(3)若直线CE、AB交于点F,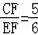
 ,CD=4,求BD的长.
,CD=4,求BD的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
为了让学生更好地进行体育锻炼,某校开展了“大课间”体育活动.为便于管理与场地安排,学校以小明所在班级为例,对学生参加各个体育项目进行了调查统计.并把调查的结果绘制了如下图所示的不完全统计图,请你根据下列信息回答问题:
(1)在这次调查中,小明所在的班级参加篮球项目的同学有多少人?并补全条形统计图.
(2)如果学校有800名学生,请估计全校学生中有多少人参加篮球项目.
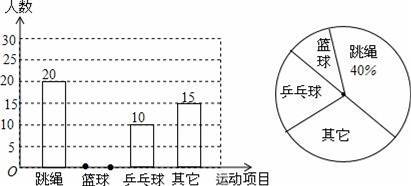

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0),则方程ax2+bx+c=0(a≠0)的两根是 .
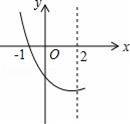

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com