
【题目】综合与探究
如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在
在![]() 轴上运动.
轴上运动.
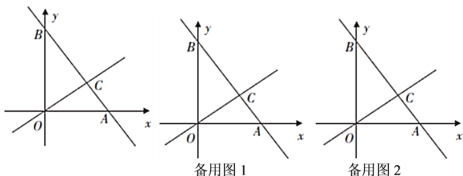
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)求使![]() 的周长最小时点
的周长最小时点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?如果存在,直接写出点
为直角边的直角三角形?如果存在,直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)P
;(2)P![]() ;(3)满足条件的点
;(3)满足条件的点![]() ,
,![]()
【解析】
(1)设直线![]() 的函数表达式为
的函数表达式为![]() ,将
,将![]() ,
,![]() 代入连立方程组求解即可;
代入连立方程组求解即可;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小,即
最小,即![]() 的周长最小,设直线
的周长最小,设直线![]() 的函数表达式为
的函数表达式为![]() ,代入C点坐标求得函数关系式,令
,代入C点坐标求得函数关系式,令![]() ,即可得到P点坐标.
,即可得到P点坐标.
(3)设CP的函数关系式为y=mx+n,当CP垂直AB时,∠PCA=90°,求得m的值,将m和C点坐标代入即可求得CP的函数关系式,即可求得P点坐标,当∠PAB=90°同理也可求解.
解:(1)设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() ,
,![]() 在直线
在直线![]() 上,
上,
![]() ,
,
解,得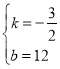 .
.
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
(2)如图,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
![]()
![]()
连接![]() 交
交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小,即
最小,即![]() 的周长最小;
的周长最小;
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() ,
,
![]() ,
,
解得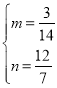
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]()
令![]() ,得
,得![]() ,
,
![]()

(3)设CP的函数关系式为y=mx+n
当CP垂直AB时,∠PCA=90°,
kab×m=-1,
∴m=![]() ,
,
将m=![]() ,
,![]() 代入y=mx+n可得
代入y=mx+n可得
n=-1,
∴CP:![]()
当x=0时,y=-1,
即P1的坐标为![]() ,
,
设CA的函数关系式为y=cx+d,
当CA垂直AB时,∠PAB=90°,
kab×c=-1,
∴c=![]() ,
,
将c=![]() ,
,![]() 代入y=cx+d可得
代入y=cx+d可得
d=![]() ,
,
∴CA:![]()
当x=0时,y=![]() -1,
-1,
即P2的坐标为![]() ,
,
∴满足条件的点![]() ,
,![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(4,6),直线y=kx+3k将平行四边形OABC分割成面积相等的两部分,则k的值是( ).

A.![]() B.
B.![]() C.-
C.-![]() D.﹣
D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=![]() x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)求抛物线的解析式;
(2)若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
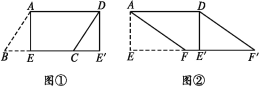
【题目】(1)如图①,在平行四边形纸片ABCD中,AD=5,SABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,判断四边形AEE'D的形状;
(2)如图②,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“滴滴出行”改变了传统打车方式,最大化节省了司机与乘客双方的资源与时间.该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元
元![]() 公里计算,耗时费按
公里计算,耗时费按![]() 元
元![]() 分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:
分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:

平均速度(公里/时) | 里程数(公里) | 车费(元) | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
(1)求![]() ,
,![]() 的值;
的值;
(2)如果你采用“滴滴出行”的打车方式,保持平均车速![]() 公里
公里![]() 时,行驶了
时,行驶了![]() 公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元
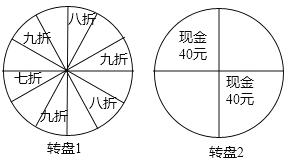
(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题成立的有( )
①勾股数是三个正整数 ②全等三角形的三条对应边分别相等
③如果两个实数相等,那么它们的平方相等 ④平行四边形的两组对角分别相等
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′,并使其面积为矩形ABCD面积的一半,若A′D′与CD交于点E,且AB=2,则△ECD′的面积是_____.
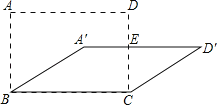
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com