
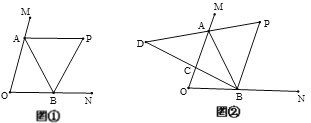
【题目】如图①,∠MON=70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
(1)点A、B在运动过程中,∠P的大小会变吗?如果不会,求出∠P的度数;如果会,请说明理由.
(2)如图②,继续作BC是平分![]() ,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
(3)如图②,∠P和∠D有怎样的数量关系?(直接写出答案)
【答案】(1)不会,∠P=55°;(2)不会,∠D=35°;(3)∠P+∠D=90°.
【解析】
(1)先根据∠MON可求出∠OAB+∠OBA的度数,再根据∠MAB与∠NBA的平分线求出∠PAB+∠PBA的度数,即可求出∠P的度数;(2)根据BC是平分![]() ,BP平方∠ABN,可求出∠DBP=90°,故可在直角三角形BDP中求出∠D(3)根据直角三角形BDP即可得出∠P和∠D的关系.
,BP平方∠ABN,可求出∠DBP=90°,故可在直角三角形BDP中求出∠D(3)根据直角三角形BDP即可得出∠P和∠D的关系.
(1)∵∠MON=70°,∴∠OAB+∠OBA=110°,
∴∠MAB+∠NBA=360°-(∠OAB+∠OBA)=250°,
∵∠MAB与∠NBA的平分线交于点P
∴∠PAB+∠PBA=![]() (∠MAB+∠NBA)=125°,
(∠MAB+∠NBA)=125°,
∴∠P=180°-(∠PAB+∠PBA)=55°.
(2)∵BC是平分![]() ,BP平方∠ABN,
,BP平方∠ABN,
∴∠DBP=![]() ∠ABN+
∠ABN+![]() ∠ABO=
∠ABO=![]() (∠ABN+∠ABO)=90°,
(∠ABN+∠ABO)=90°,
∴∠D=90°-∠P=35°,
(3)∵△BDP为直角三角形,故∠P+∠D=90°.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
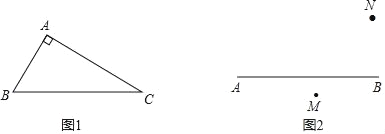
【题目】(1)如图1,在Rt△ABC中,AB=3,AC=4,BC=5,若直线EF垂直平分BC,请你利用尺规画出直线EF;
(2)若点P在(1)中BC的垂直平分线EF上,请直接写出PA+PB的最小值,回答PA+PB取最小值时点P的位置并在图中标出来;
解:PA+PB的最小值为 ,PA+PB取最小值时点P的位置是 ;
(3)如图2,点M,N分别在直线AB两侧,在直线AB上找一点Q,使得∠MQB=∠NQB.要求画图,并简要叙述确定点Q位置的步骤(无需尺规作图,保留画图痕迹,无需证明)
解:确定点Q位置的简要步骤: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.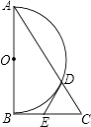
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
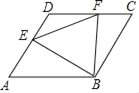
【题目】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(![]() ),王红家只有刻度不超过
),王红家只有刻度不超过![]() 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔![]() 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A. 没有加热时,油的温度是![]()
B. 加热![]() ,油的温度是
,油的温度是![]()
C. 估计这种食用油的沸点温度约是![]()
D. 每加热![]() ,油的温度升高
,油的温度升高![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.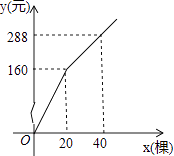
(1)求y与x的函数关系式;
(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A种树苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com