
【题目】一个不透明口袋中装有5个白球和6个红球,这些球除颜色外完全相同,充分搅匀后随机摸球.
(1)如果先摸出一白球,将这个白球放回,再摸出一球,那么它是白球的概率是多少?
(2)如果先摸出一白球,这个白球不放回,再摸出一球,那么它是白球的概率是多少?
(3)如果先摸出一红球,这个红球不放回,再摸出一球,那么它是白球的概率是多少?
【答案】(1)它是白球的概率是P=![]() ;(2)它是白球的概率是P=
;(2)它是白球的概率是P=![]() =
=![]() ;(3)它是白球的概率是P=
;(3)它是白球的概率是P=![]() =
=![]() .
.
【解析】
(1)摸出一个白球放回对第二次摸到白球没有影响,直接利用概率公式求解即可;
(2)如果这个白球不放回,则总数减少1,白球数减少1,再利用概率公式求解即可;
(3)如果这个红球不放回,则总数减少1,红球数减少1,再利用概率公式求解即可.
(1)先摸出一白球,将这个白球放回,那么第二次模球时,仍然有5个白球和6个红球,则再摸出一球,那么它是白球的概率是P=![]() ;
;
(2)先摸出一白球,这个白球不放回,那么第二次摸球时,有4个白球和6个红球,那么它是白球的概率是P=![]() =
=![]() ;
;
(3)先摸出一红球,这个红球不放回,那么第二次摸球时,有5个白球和5个红球,那么它是白球的概率是P=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项![]() ,因式分解的结果是
,因式分解的结果是![]() ,若取
,若取![]() ,
,![]() 时,则各个因式的值是:
时,则各个因式的值是:![]() ,
,![]() ,
,![]() ,于是就可以把“180162”作为一个六位数的密码,对于多项式
,于是就可以把“180162”作为一个六位数的密码,对于多项式![]() ,取
,取![]() ,
,![]() 时,用上述方法产生的密码是________ (写出一个即可).
时,用上述方法产生的密码是________ (写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
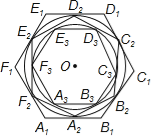
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个正方形的边长都为1的正方形网格中,点![]() 都在格点上,从这四个点中任取三个点构成三角形,则构成的三角形中,不是直角三角形的是( )
都在格点上,从这四个点中任取三个点构成三角形,则构成的三角形中,不是直角三角形的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com