
【题目】如图,二次函数 ![]() 的图像与
的图像与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,
, ![]() .点
.点 ![]() 在函数图像上,
在函数图像上, ![]() 轴,且
轴,且 ![]() ,直线
,直线 ![]() 是抛物线的对称轴,
是抛物线的对称轴, ![]() 是抛物线的顶点.
是抛物线的顶点.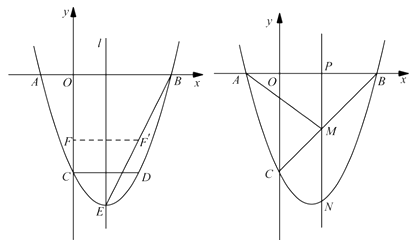
图 ① 图②
(1)求 ![]() 、
、 ![]() 的值;
的值;
(2)如图①,连接 ![]() ,线段
,线段 ![]() 上的点
上的点 ![]() 关于直线
关于直线 ![]() 的对称点
的对称点 ![]() 恰好在线段
恰好在线段 ![]() 上,求点
上,求点 ![]() 的坐标;
的坐标;
(3)如图②,动点 ![]() 在线段
在线段 ![]() 上,过点
上,过点 ![]() 作
作 ![]() 轴的垂线分别与
轴的垂线分别与 ![]() 交于点
交于点 ![]() ,与抛物线交于点
,与抛物线交于点 ![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点 ![]() ,使得
,使得 ![]() 与
与 ![]() 的面积相等,且线段
的面积相等,且线段 ![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点 ![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
【答案】
(1)
解:∵CD⊥x轴,CD=2,
∴抛物线对称轴为直线l:x=1,
∴![]() =1,则b=-2。
=1,则b=-2。
∵OB=OC,C(0,c),
∴B点的坐标为(-c,0),
∴0=c2+2c+c,解得c=-3或c=0(舍去),
∴c=-3,
(2)
解:由(1)可得抛物线解析式为y=x2-2x-3,则E(1,-4)
设点F的坐标为(0,m),
∵对称轴为直线l:x=1,
∴点F关于直线l的对称点F的坐标为(2,m)。
∵直线BE经过点B(3,0),E(1,-4),
∴利用待定系数法可得直线BE的表达式y=2x-6,
∵点F在BE上,
∴m=2×2-6=-2,
即点F的坐标为(0,-2)。
(3)
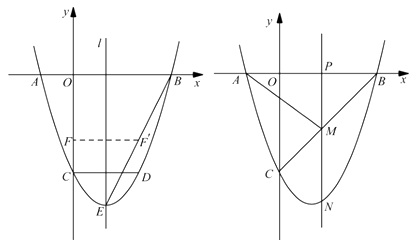
解:存在点Q满足题意。设点P坐标为(n,0),则PA=n+1,PB=PM=3-n,PN=-n2+2n+3,
作QR⊥PN,垂足为R,
∵S△PQN=S△APM,
∴![]() (n+1)(3-n)=
(n+1)(3-n)=![]() (-n2+2n+3)QR,
(-n2+2n+3)QR,
∴QR=1。
①点Q在直线PN的左侧时,Q点的坐标为(n-1,n2-4n),R点的坐标为(n,n2-4n),N点的坐标为(n,n2-2n-3),
∴在Rt△QRN中,NQ2=1+(2n-3)2,
∴n=![]() 时,NQ取最小值1,此时Q点的坐标为(
时,NQ取最小值1,此时Q点的坐标为(![]() ,
,![]() )
)
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).
同理NQ2=1+(2n-1)2,
∴n=![]() 时,NQ取最小值1,此时Q点的坐标为(
时,NQ取最小值1,此时Q点的坐标为(![]() ,
,![]() ).
).
综上所述,满足题意的点Q的坐标为(![]() ,
,![]() )和(
)和(![]() ,
,![]() )
)
【解析】(1)因为CD⊥x轴,所以C与D的纵坐标相等,即C与D关于抛物线的对称轴对称,则可得对称轴是直线l:x=1,从而由x=-![]() 代入a的值,求出b;又由OB=OC,可得B(-c,0),代入二次函数解析式,求出c的值即可;
代入a的值,求出b;又由OB=OC,可得B(-c,0),代入二次函数解析式,求出c的值即可;
(2)设点F的坐标为(0,m)关于直线x=1的对称点为(2,m),则求出BE的解析式,将(2,m)代入解出m的值即可;
(3)可设P(n,0),用n可表示出PA=n+1,PB=PM=3-n,PN=-n2+2n+3,作QR⊥PN,垂足为R,由S△PQN=S△APM , 可列出方程求出QR=1;
分类讨论点Q在直线PN的左侧和Q在直线PN的右侧时,在Rt△QRN中,由勾股定理可得NQ2=QR2+NR2,求出当n为多少时,NQ为最小值,写出相对应的Q的坐标。
【考点精析】掌握二次函数的图象和三角形的面积是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;三角形的面积=1/2×底×高.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) 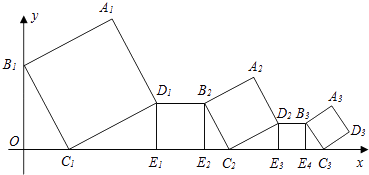
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
特殊网图 |
|
|
|
|
结点数(V) | 4 | 6 | 9 | 12 |
网眼数(F) | 1 | 2 | 4 | 6 |
边数(E) | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为_____;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为___ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点.过点
的中点.过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() .将
.将 ![]() 沿点
沿点 ![]() 到点
到点 ![]() 的方向平移,得到
的方向平移,得到 ![]() .设
.设 ![]() 、
、 ![]() 分别是
分别是 ![]() 、
、 ![]() 的中点,当点
的中点,当点 ![]() 与点
与点 ![]() 重合时,四边形
重合时,四边形 ![]() 的面积为( )
的面积为( )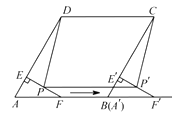
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() 轴,垂足为
轴,垂足为 ![]() .反比例函数
.反比例函数 ![]() (
( ![]() )的图像经过点
)的图像经过点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.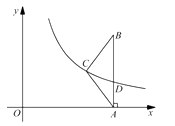
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)连接 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
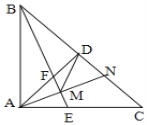
【题目】如图,等腰![]() 中,
中,![]() =90°,
=90°,![]() 于
于![]() ,
,![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④![]() ;上述结论中正确的个数是( )
;上述结论中正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值: 2(m2 mn 1) 3(![]() m2 2mn 4) ,其中 m
m2 2mn 4) ,其中 m ![]() ,n 3 .
,n 3 .
(2)已知 2a b 5 0 ,求整式 6a b 与 2a 3b 27 的和的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com