
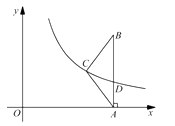
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() 轴,垂足为
轴,垂足为 ![]() .反比例函数
.反比例函数 ![]() (
( ![]() )的图像经过点
)的图像经过点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)连接 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)
解:过点C作CD⊥AB于E,
因为AC=BC,
所以AE=BE=2,
在Rt△BCE中,CE=![]() ,
,
则点C的横坐标为4-![]() ,
,
即C(![]() ,2)。
,2)。
将点C(![]() ,2)代入y=
,2)代入y=![]() ,得k=5。
,得k=5。
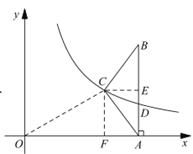
(2)
解:设A点的坐标为(m,0).
因为BD=BC=![]()
所以AD=![]()
则D,C两点的坐标分别为(m,![]() ),(m-
),(m-![]() ,2) .
,2) .
因为点D,C都在y=![]() 的图象上,
的图象上,
所以![]() ,
,
所以m=6
所以点C的坐标为(![]() ,2)
,2)
作CF⊥x轴,垂足为F.在Rt△OCF中,
OC=![]() .
.

【解析】(1)求点C的坐标,过点C作CD⊥AB于E,则AE=BE=2,由勾股定理求出CE,则求得点C的坐标,代入反比例函数即可解得;
(2)求点C的坐标,设A点的坐标为(m,0),由BD=BC=![]() ,可得D的纵坐标为AD=
,可得D的纵坐标为AD=![]() ,则D(m,
,则D(m,![]() ),C(m-
),C(m-![]() ,2) .由点D,C都在y=
,2) .由点D,C都在y=![]() 的图象上,,可求出m的值,即而求出点C的坐标,根据勾股定理即可求OC的长。
的图象上,,可求出m的值,即而求出点C的坐标,根据勾股定理即可求OC的长。
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
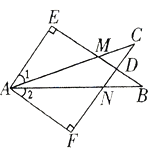
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水是人类的生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的沿湖道路 ![]() 上有
上有 ![]() 、
、 ![]() 两个游船码头,观光岛屿
两个游船码头,观光岛屿 ![]() 在码头
在码头 ![]() 北偏东
北偏东 ![]() 的方向,在码头
的方向,在码头 ![]() 北偏西
北偏西 ![]() 的方向,
的方向, ![]()
![]() .游客小张准备从观光岛屿
.游客小张准备从观光岛屿 ![]() 乘船沿
乘船沿 ![]() 回到码头
回到码头 ![]() 或沿
或沿 ![]() 回到码头
回到码头 ![]() ,设开往码头
,设开往码头 ![]() 、
、 ![]() 的游船速度分别为
的游船速度分别为 ![]() 、
、 ![]() ,若回到
,若回到 ![]() 、
、 ![]() 所用时间相等,则
所用时间相等,则 ![]() (结果保留根号).
(结果保留根号).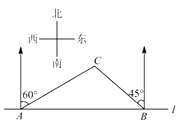
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图像与
的图像与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,
, ![]() .点
.点 ![]() 在函数图像上,
在函数图像上, ![]() 轴,且
轴,且 ![]() ,直线
,直线 ![]() 是抛物线的对称轴,
是抛物线的对称轴, ![]() 是抛物线的顶点.
是抛物线的顶点.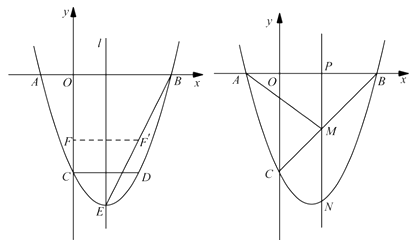
图 ① 图②
(1)求 ![]() 、
、 ![]() 的值;
的值;
(2)如图①,连接 ![]() ,线段
,线段 ![]() 上的点
上的点 ![]() 关于直线
关于直线 ![]() 的对称点
的对称点 ![]() 恰好在线段
恰好在线段 ![]() 上,求点
上,求点 ![]() 的坐标;
的坐标;
(3)如图②,动点 ![]() 在线段
在线段 ![]() 上,过点
上,过点 ![]() 作
作 ![]() 轴的垂线分别与
轴的垂线分别与 ![]() 交于点
交于点 ![]() ,与抛物线交于点
,与抛物线交于点 ![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点 ![]() ,使得
,使得 ![]() 与
与 ![]() 的面积相等,且线段
的面积相等,且线段 ![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点 ![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数 1 至 1050 按一定规律排列如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 | 16 | 17 | 18 | 19 | 20 | 21 |
22 | 23 | 24 | 25 | 26 | 27 | 28 |
29 | 30 | 31 | 32 | 33 | 34 | 35 |
从表中任取一个 3 3 的方框(如表中带阴影的部分),方框中九个数的和可能是( )
A. 2025 B. 2018 C. 2016 D. 2007
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
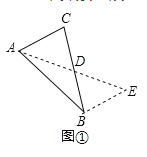

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com