
【题目】如图所示,AB⊥BC且AB=BC,CD⊥DE且CD=DE,请按照图中所标注的数据,计算图中实线所围成的图形面积是( )
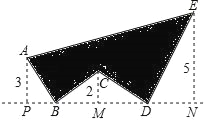
A. 64 B. 50 C. 48 D. 32
【答案】D
【解析】
先证△ABP≌△BCM(AAS),得AP=BM=3,BP=CM=2,同理可得CM=DN=2,DM=EH=5,得PN=12,再求梯形AENP的面积=![]() ×(AP+EN)×PN=
×(AP+EN)×PN=![]() ×(3+5)×12=48,
×(3+5)×12=48,
由阴影部分的面积=S梯形AENP﹣S△ABP﹣S△BCD﹣S△DEN,可得结果.
作CM⊥DB,AP⊥BD,EN⊥BD,
∵AB⊥BC,
∴∠APB=∠BMC=∠ABC=90°,
∴∠ABP+∠BAP=90°,∠ABP+∠CBM=90°,
∴∠BAP=∠CBM,
在△ABP和△BCM中
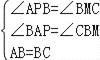 ,
,
∴△ABP≌△BCM(AAS),
∴AP=BM=3,BP=CM=2,
同理可得CM=DN=2,DM=EH=5,
∴PN=12,
∴梯形AENP的面积=![]() ×(AP+EN)×PN=
×(AP+EN)×PN=![]() ×(3+5)×12=48,
×(3+5)×12=48,
∴阴影部分的面积=S梯形AENP﹣S△ABP﹣S△BCD﹣S△DEN
=48﹣![]() ×3×2﹣
×3×2﹣![]() ×(3+5)×2﹣
×(3+5)×2﹣![]() ×5×2
×5×2
=48﹣3﹣8﹣5
=32.
故选:D


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点. 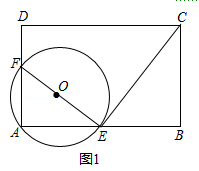
(1)求证:圈O与CE相切与点E;
(2)如图1,若AF=2FD且∠AEF=30°,求n的值; 
(3)如图2.若EF=EC且圈O与边CD相切,求n的值. 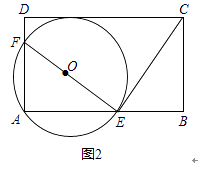
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;……;则第10个图形中,其中看得见的小立方体个数是( )
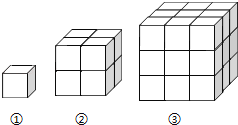
A. 270 B. 271 C. 272 D. 273
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.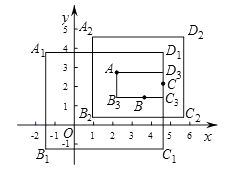
(1)已知A( ![]() 2,3),B(5,0),C(
2,3),B(5,0),C( ![]() ,
, ![]() 2).
2).
①当 ![]() 时,点A,B,C的最优覆盖矩形的面积为;
时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为;
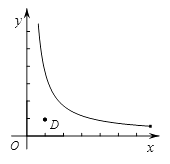
(2)已知点D(1,1),点E( ![]() ,
, ![]() ),其中点E是函数
),其中点E是函数 ![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足(b﹣3)2+|c+4|=0,且a,b,c分别是点A,B,C在数轴上对应的数.
![]()
(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
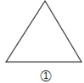



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com