
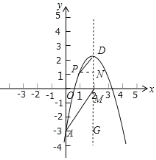
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a+3(a<0)的顶点为D,它的对称轴与x轴交点为M.
(1)求点D、点M的坐标;
(2)如果该抛物线与y轴的交点为A,点P在抛物线上,且有MA∥DP,DP=![]() AM,求该抛物线解析式.
AM,求该抛物线解析式.
【答案】(1)D(2,3),M(2,0);(2)y=﹣![]() x2+6x﹣3
x2+6x﹣3
【解析】
(1)由y=ax2-4ax+4a+3=a(x-2)2+3,即可得到顶点D(2,3),M(2,0);(2)作PN⊥DM于N,由△PDN∽△MAO,得![]() 由OM=2,OA=-4a-3,PN=1,故P(1,a+3),DN=-a,根据OA=2DN,可得方程-4a-3=-2a,即可解出a的值.
由OM=2,OA=-4a-3,PN=1,故P(1,a+3),DN=-a,根据OA=2DN,可得方程-4a-3=-2a,即可解出a的值.
解:(1)∵y=ax2-4ax+4a+3=a(x-2)2+3,
∴顶点D(2,3),M(2,0);
(2)作PN⊥DM于N,
∵AM∥DP,∴∠PDN=∠AMG,
∵DG∥OA,
∴∠OAM=∠AMG=∠PDN,
∵∠PND=∠MAO=90°,
∴△PDN∽△MAO,
∴![]()
∵OM=2,OA=-4a-3,PN=1,
∴P(1,a+3)
∴DN=-a,
∵OA=2DN,
∴-4a-3=-2a,
a=-![]()
∴解析式为y=﹣![]() x2+6x﹣3
x2+6x﹣3


科目:初中数学 来源: 题型:
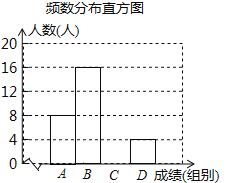
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
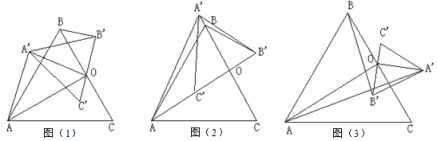
【题目】操作:![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() 绕着
绕着![]() 点按顺时针方向旋转,
点按顺时针方向旋转,![]() 是
是![]() 、
、![]() 的中点,有以下三种图形.
的中点,有以下三种图形.
探究:
(1)在上述三个图形中,![]() 是否一个固定的值,若是,请选择任意一个图形求出这个比值;
是否一个固定的值,若是,请选择任意一个图形求出这个比值;
(2)![]() 的值是否也等于这个定值,若是,请结合图(1)证明你的结论;
的值是否也等于这个定值,若是,请结合图(1)证明你的结论;
(3)![]() 与
与![]() 有怎样的位置关系,请你结合图(2)或图(3)证明你的结论.
有怎样的位置关系,请你结合图(2)或图(3)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
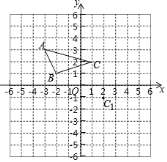
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,3),B(-2,1),C(1,2).
(1)把△ABC绕原点O旋转,使点C与点C1(2,-1)重合,画出旋转后的△A1B1C1,并写出点A1,B1的坐标;
(2)在(1)的条件下,若△ABC是按顺时针方向旋转的,求点A到点A1经过的路径![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
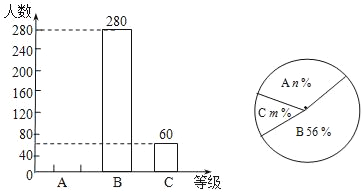
(1)本次调查的人数为 ;
(2)补全条形统计图;
(3)若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
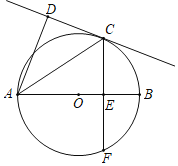
【题目】如图已知AB为⊙O的直径,CD切⊙O于C点,弦CF⊥AB于E点,连结AC.
(1)探索AC满足什么条件时,有AD⊥CD,并加以证明.
(2)当AD⊥CD,OA=5cm,CD=4cm,求△OCF面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.

(1)求证:△CAE∽△CBF
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
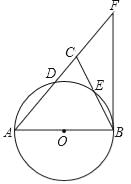
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC、BC于点D、E,过点B作直线BF,交AC的延长线于点F.
(1)求证:BE=CE;
(2)若AB=6,求弧DE的长;
(3)当∠F的度数是多少时,BF与⊙O相切,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
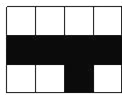
【题目】如图,共有12个大不相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com