Question

2．如图，在△ABC中，BD平分∠ABC，
（1）作图：作BC边的垂直平分线分别交BC，BD于点E，F（用尺规作图法，保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，连结CF，若∠A=60°，∠ABD=24°，求∠ACF的度数．

Answer 1

分析 （1）分别以B、C为圆心，大于$\frac{1}{2}$BC长为半径画弧，两弧交于两点，过两点画直线，与BC，BD的交点记作E，F；
（2）根据角平分线性质可得∠ABC=2∠ABD，∠ABD=∠CBD，然后利用三角形内角和定理可得∠ACB的度数，根据线段垂直平分线的性质可得BF=CF，进而可得∠FCB=∠FBC=24°，再根据角的和差关系可得答案．

解答 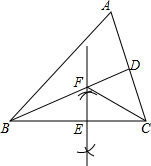解：（1）如图所示：

（2）∵BD平分∠ABC，
∴∠ABC=2∠ABD，∠ABD=∠CBD，
∵∠ABD=24°，
∴∠ABC=48°，∠DBC=24°，
∵∠A=60°，
∴∠ACB=180°-60°-48°=72°，
∵EF是BC的垂直平分线，
∴BF=CF，
∴∠FCB=∠FBC=24°，
∴∠ACF=72°-24°=48°．

点评 此题主要考查了复杂作图，以及线段垂直平分线的性质，三角形内角和定理，角平分线的性质，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．