
【题目】如图,已知,∠AOE=∠COD,且射线OC平分∠EOB,∠EOD=30°. 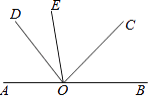
(1)试说明∠AOD=∠BOC;
(2)求∠AOD的度数.
【答案】
(1)解:∵∠AOE=∠COD,
∴∠AOE﹣∠DOE=∠COD﹣∠DOE
∴∠AOD=∠COE,
∵OC平分∠EOB,
∴∠BOC=∠COE,
∴∠AOD=∠BOC,
(2)解:设∠AOD=α,
∴∠AOD=∠BOC=∠COE=α,
∴∠AOD+∠DOE+∠COE+∠BOC=180°,
∴3α+30°=180°,
∴α=50°,
∴∠AOD=50°
【解析】(1)因为∠AOE=∠COD,所以∠AOD=∠COE,由于OC平分∠EOB,所以∠BOC=∠COE,从而得证.(2)设∠AOD=α,根据∠AOD+∠DOE+∠COE+∠BOC=180°,即可求出α的值.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


科目:初中数学 来源: 题型:
【题目】某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,求该种干果的第一次进价是每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为 . 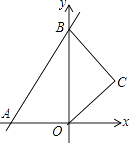
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,又∵(m﹣n)2≥0,(n﹣4)2≥0,
∴ ![]() ,∴n=4,m=4.
,∴n=4,m=4.
请解答下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy﹣x2的值;
(2)已知△ABC的三边长a、b、c都是互不相等的正整数,且满足a2+b2﹣4a﹣18b+85=0,求△ABC的最大边c的值;
(3)已知a2+b2=12,ab+c2﹣16c+70=0,求a+b+c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com