
【题目】已知:AB为⊙O的直径,弦CD⊥AO,垂足为点E,连接AD,点N是AD上一点,连接CN交AE于点F,延长CN交⊙O与点M,连接AM,MD.
(1)如图1,求证:∠AMC=∠MCD+∠ADM;
(2)如图2,连接BC,过点A作AG⊥AD交⊙O与点G,求证:AG=BC;
(3)如图3,在(2)的条件下,AN=ND,延长CM至点K,MK=2MN=6,FE=3,连接KA,GC,并延长KA,GC交于点H,求HG的长.
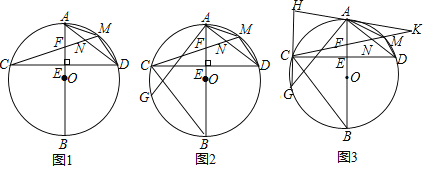
【答案】(1)证明见解析;(2)证明见解析;(3)HG=![]() .
.
【解析】
(1)连接AC,AB为⊙O的直径,弦CD⊥AO,得![]() ,∠ADC=∠ACM+∠MCD,再由同弧所对的圆周角相等即可得证;
,∠ADC=∠ACM+∠MCD,再由同弧所对的圆周角相等即可得证;
(2)根据等角的余角相等可得:∠ABC=∠BAG,再根据同圆中,相等的圆周角所对的弧相等可得:![]() ,易证结论;
,易证结论;
(3)过点D作DR∥AE交CK于R,易证:△ANF≌△DNR(ASA),得到:AF=DR=6,再过点A作AT∥DM交CM于点T,求得TA=TM=MD=MK=6,过点O作OW⊥MD,连接OM,OD,OC,可求得FE=OE=3,OC=CF=OA=12,AK=AD=6![]() ,过点N作NL⊥AK于点L,设AL=a,通过构建方程求a,可求得:sin∠HAG=sin∠LNA=
,过点N作NL⊥AK于点L,设AL=a,通过构建方程求a,可求得:sin∠HAG=sin∠LNA=![]() ,最后过点H作HQ⊥AG于点Q,设HA=8b,HQ=7b,构建方程即可得解.
,最后过点H作HQ⊥AG于点Q,设HA=8b,HQ=7b,构建方程即可得解.
(1)证明:如图1,连接AC,
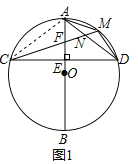
∵AB为⊙O的直径,弦CD⊥AO
∴![]()
∴∠ADC=∠ACD,即∠ADC=∠ACM+∠MCD
∵![]() ,
,![]()
∴∠ACM=∠ADM,∠ADC=∠AMC
∴∠AMC=∠ADM+∠MCD
(2)证明:∵CD⊥AO
∴∠AED=90°
∴∠BAD+∠ADC=90°
∵∠ADC=∠ABC
∴∠BAD+∠ABC=90°
∵∠BAD+∠BAG=90°
∴∠ABC=∠BAG
∴![]()
∴![]() ,即:
,即:![]()
∴AG=BC
(3)如图3,过点D作DR∥AE交CK于R,
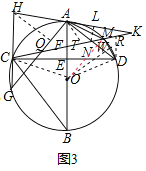
∴![]()
∵AB为直径,CD⊥AO
∴CE=DE
∴CF=FR
∴DR=2EF=2×3=6
∵DR∥AE
∴∠FAN=∠RDN
∵AN=ND,∠ANF=∠DNR
∴△ANF≌△DNR(ASA)
∴AF=DR=6
过点A作AT∥DM交CM于点T,∴∠TAN=∠MDN,
∵AN=ND,∠ANT=∠DNM
∴△ANT≌△DNM(ASA)
∴TA=MD,TN=MN
∵2MN=MK
∴2TN=2MN=TM=MK=6
∵![]()
∴∠MAD=∠MCD
∵∠AMC=∠ADM+∠MCD
∴∠AMC=∠TAN+∠MAD=∠TAM
∴TA=TM=MD=MK=6
过点O作OW⊥MD,连接OM,OD,OC,∵OM=OD
∴MW=DW=![]() MD=3,∠MOW=∠DOW=
MD=3,∠MOW=∠DOW=![]() ∠MOD
∠MOD
∴FE=MW=3
∵![]()
∴2∠DCM=∠MOD
∴∠MCD=∠MOW=∠DOW
∵∠FEC=∠MWO=90°
∴△FEC≌△MWO(AAS)
∴OM=CF=OC
∴FE=OE=3,OC=CF=OA=3+3+6=12
在Rt△CEF中,![]() ,
,
在Rt△AED中,![]() ,
,
在Rt△BCE中,![]() ,
,
∵∠AMD=180°﹣∠MDA﹣∠MAD=180°﹣∠AMC=∠AMK,AM=AM,MD=MK
∴△AMD≌△AMK(SAS)
∴AK=AD=6![]()
过点N作NL⊥AK于点L,则∠ALN=90°,设AL=a,LK=6![]() ﹣a,
﹣a,
∵AN=ND=![]() AD=3
AD=3![]() ,NK=3+6=9,NL2=AN2﹣AL2=NK2﹣KL2,
,NK=3+6=9,NL2=AN2﹣AL2=NK2﹣KL2,
∴![]() ,解得:
,解得:![]() ,
,
∵∠GAD=90°,∠LAN+∠LNA=90°=∠LAN+∠HAG
∴∠HAG=∠LNA
∴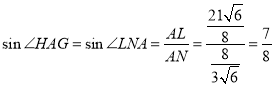 ,
,
过点H作HQ⊥AG于点Q,
设HA=8b,HQ=7b,则![]() ,
,
∵AG=BC=6![]() ,
,
∴QG=6![]() ﹣
﹣![]() b
b
∵∠AGC=∠ABC
∴tan∠AGC=tan∠ABC
∴![]() ,解得:b=
,解得:b=![]() ,
,
∴![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
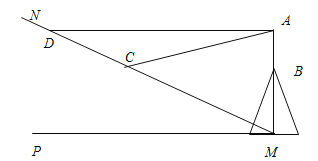
【题目】如图所示.在山顶上有一座电视塔AB(AB与水平面垂直),小明同学要测量电视塔AB的高度,在斜坡MN上取一点C,测得塔顶A的仰角为15°,小明沿斜坡MN上行300米到点D,在点D恰好平视电视塔顶A(即AD与水平地面平行),若斜坡MN的坡角为30,山高BM为400米,且N、D、C、M、P、B、A在同一平面内,A、B、M在同一条直线上,请根据以上数据帮助小明求出电视塔AB的高度(结果精确到1米)(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
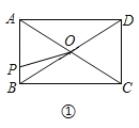
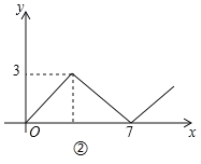
【题目】如图①,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,动点
,动点![]() 由点
由点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.设点
运动.设点![]() 的运动路程为
的运动路程为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系图象如图②所示,则
的函数关系图象如图②所示,则![]() 边的长为( ).
边的长为( ).
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
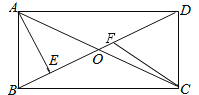
【题目】如图,矩形ABCD中,AC与BD交于点O,AE⊥BD,垂足为E,点F在线段OD上,∠EAO=∠FCB,AE=EF=4,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.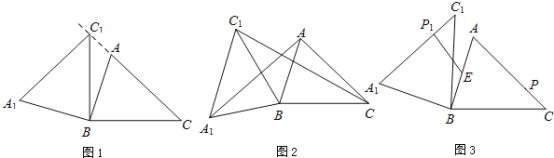
查看答案和解析>>
科目:初中数学 来源: 题型:
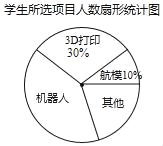
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
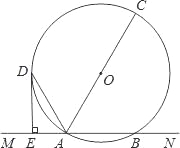
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆O交AC于点D,交BC于点E,以点B为顶点作∠CBF,使得∠CBF=![]() ∠BAC,交AC延长线于点F连接BD、AE,延长AE交BF于点G,
∠BAC,交AC延长线于点F连接BD、AE,延长AE交BF于点G,
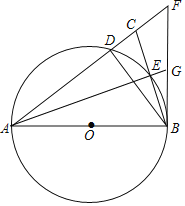
(1)求证:BF为⊙O的切线;(2)求证:ACBC=BDAG;(3)若BC=2![]() ,CD:CF=4:5,求⊙O的半径.
,CD:CF=4:5,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com