
【题目】如图所示.在山顶上有一座电视塔AB(AB与水平面垂直),小明同学要测量电视塔AB的高度,在斜坡MN上取一点C,测得塔顶A的仰角为15°,小明沿斜坡MN上行300米到点D,在点D恰好平视电视塔顶A(即AD与水平地面平行),若斜坡MN的坡角为30,山高BM为400米,且N、D、C、M、P、B、A在同一平面内,A、B、M在同一条直线上,请根据以上数据帮助小明求出电视塔AB的高度(结果精确到1米)(![]() )
)
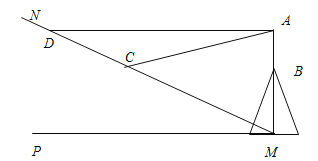
【答案】电视塔AB的高度73米.
【解析】
先过C作CF⊥AB于F,过A作AE⊥DC于E,根据角度关系可得AE=CE,设AE=CE=x,则DE=300+x,在Rt△ADE中可得DE=![]() ,所以 300+x=
,所以 300+x=![]() ,可求出x的值,在Rt△AEM中AM=
,可求出x的值,在Rt△AEM中AM=![]() ,可计算出AM的值,已知BM=400,近一步求出AB的值即可解答.
,可计算出AM的值,已知BM=400,近一步求出AB的值即可解答.
解:如图,过C作CF⊥AB于F,过A作AE⊥DC于E,

∵塔顶A的仰角为15°,斜坡MN的坡角为30,
∴∠ACE=45°,∠ADE=30°,∠AME=60°,
三角形ACE是等腰直角三角形,设AE=CE=x,则DE=300+x,
在Rt△ADE中∠ADE=30°,可得DE=![]() =
=![]() ,
,
∴300+x=![]() ,解得x=150(
,解得x=150(![]() ),
),
在Rt△AEM中∠AME=60°,可得AM=![]() =
=![]() =100(3+
=100(3+![]() ),
),
所以AB=AM-BM=100(3+![]() )-400≈73(m);
)-400≈73(m);
答:电视塔AB的高度为73m.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某大型超市为了缓解停车难的问题,建筑设计师提供了楼顶停车场的设计示意图(如图AC与ME平行).按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.请根据下图求出汽车通过坡道口的限高DF的长.(结果精确到0.1m)
(参考数据: sin28°≈0.47,cos28°≈0.88, tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
(2)若B型号足球数量不少于A型号足球数量的![]() ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.
(1)求证:AC平分BAD;
(2)若AC=![]() ,CD=2,求⊙O的直径.
,CD=2,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).

(1)将△ABC沿![]() 轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点O顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2 、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分.
学 生 类 型 人数 时间 |
|
|
|
|
| |
性别 | 男 | 7 | 31 | 25 | 30 | 4 |
女 | 8 | 29 | 26 | 32 | 8 | |
学段 | 初中 | 25 | 36 | 44 | 11 | |
高中 | ||||||

下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5-25.5之间
②这200名学生参加公益劳动时间的中位数在20-30之间
③这200名学生中的初中生参加公益劳动时间的中位数一定在20-30之间
④这200名学生中的高中生参加公益劳动时间的中位数可能在20-30之间
所有合理推断的序号是( )
A. ①③B. ②④C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() 与直线
与直线![]() ,直线
,直线![]() 分别交于点A,B,直线
分别交于点A,B,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,结合函数图象,求区域
时,结合函数图象,求区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内没有整点,直接写出
内没有整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司其有![]() 名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.
名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.
频率分布表
组别 | 销售数量(件) | 频数 | 频率 |
A |
|
|
|
B |
|
|
|
C |
|
|
|
D |
|
|
|
E |
|
|
|
合计 |
|
| |
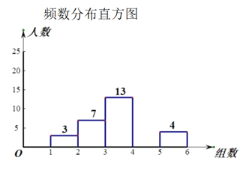
请根据以上信息,解决下列问题:
(1)频数分布表中,![]() ________、
________、![]() ________:
________:
(2)补全频数分布直方图;
(3)如果该季度销量不低于![]() 件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
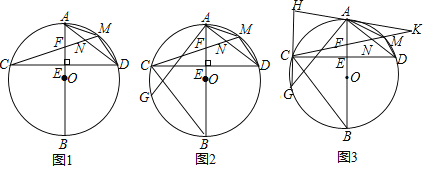
【题目】已知:AB为⊙O的直径,弦CD⊥AO,垂足为点E,连接AD,点N是AD上一点,连接CN交AE于点F,延长CN交⊙O与点M,连接AM,MD.
(1)如图1,求证:∠AMC=∠MCD+∠ADM;
(2)如图2,连接BC,过点A作AG⊥AD交⊙O与点G,求证:AG=BC;
(3)如图3,在(2)的条件下,AN=ND,延长CM至点K,MK=2MN=6,FE=3,连接KA,GC,并延长KA,GC交于点H,求HG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com