
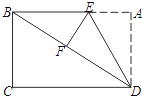
【题目】如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )
A. ![]() B. 1 C. 2 D.
B. 1 C. 2 D. ![]()
【答案】A
【解析】分析: 根据矩形对边相等可得AB=CD,再利用勾股定理列式求出BD,根据翻折的性质可得DF=AD,EF=AE,∠DFE=∠A=90°,然后求出BF,设AE=x,表示出BE,在Rt△BEF中,利用勾股定理列方程求解即可.
详解: 在矩形ABCD中,AB=CD=4,
由勾股定理得,BD=![]() =
=![]() =5,
=5,
∵矩形纸片ABCD折叠,边AD落在对角线BD上,A点落在对角线F处
∴DF=AD=3,EF=AE,∠DFE=∠A=90°,
∴BF=BD-DF=5-3=2,
设AE=x,则BE=4-x,
在Rt△BEF中,由勾股定理得,BF2+EF2=BE2,
即22+x2=(4-x)2,
解得x=![]() ,
,
即AE的长为![]() .
.
故选A.


科目:初中数学 来源: 题型:
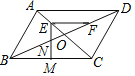
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB=OB,点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,FN=![]() ,则线段BC的长为_____.
,则线段BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
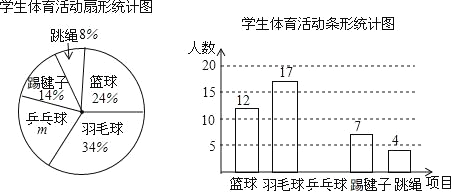
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园门票价是每人10元,公园规定:如果一次购票满30张,每张可少收2元.
(1)若某班有18名同学去公园,则需要 元;
(2)若某班有![]() 名同学去公园共需要 元;
名同学去公园共需要 元;
(3)若某班有27名同学去公园,怎样买票更合算?最少需要多少元?
(4)若某班去公园共交费240元,则该班可能有多少人去公园?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
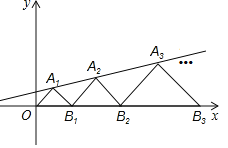
【题目】如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ]= ;[
]= ;[![]() ]= .
]= .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
(3)如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次[![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.对145连续求根整数, 次之后结果为1.
]=1,这时候结果为1.对145连续求根整数, 次之后结果为1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com