
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
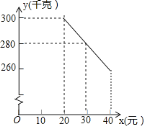
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,B、C两点的坐标分别为B(0,3)和C(0,﹣![]() ),点A在x轴正半轴上,且满足∠BAO=30°.
),点A在x轴正半轴上,且满足∠BAO=30°.
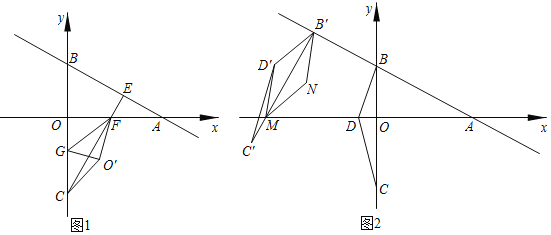
(1)过点C作CE⊥AB于点E,交AO于点F,点G为线段OC上一动点,连接GF,将△OFG沿FG翻折使点O落在平面内的点O′处,连接O′C,求线段OF的长以及线段O′C的最小值;
(2)如图2,点D的坐标为D(﹣1,0),将△BDC绕点B顺时针旋转,使得BC⊥AB于点B,将旋转后的△BDC沿直线AB平移,平移中的△BDC记为△B′D′C′,设直线B′C′与x轴交于点M,N为平面内任意一点,当以B′、D′、M、N为顶点的四边形是菱形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.

(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
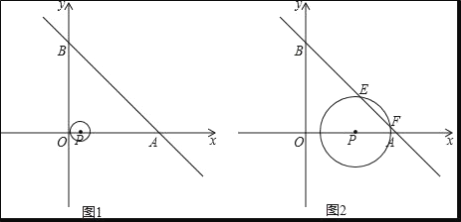
【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=![]() 时,弦EF的长;
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上,AG=CH,直线GH绕点O逆时针旋转α角,与边AB、CD分别相交于点E、F(点E不与点A、B重合).
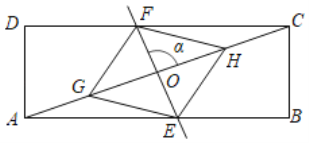
(1)求证:四边形EHFG是平行四边形;
(2)若∠α=90°,AB=9,AD=3,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
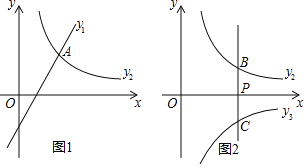
(1)如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .
.
①求![]() ,
,![]() 的值;
的值;
②直接写出当![]() 时
时![]() 的范围;
的范围;
(2)如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
①若![]() ,直线
,直线![]() 与函数
与函数![]() 的图象相交点
的图象相交点![]() .当点
.当点![]() 、
、![]() 、
、![]() 中的一点到另外两点的距离相等时,求
中的一点到另外两点的距离相等时,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的平行线与函数
轴的平行线与函数![]() 的图象相交于点
的图象相交于点![]() .当
.当![]() 的值取不大于1的任意实数时,点
的值取不大于1的任意实数时,点![]() 、
、![]() 间的距离与点
间的距离与点![]() 、
、![]() 间的距离之和
间的距离之和![]() 始终是一个定值.求此时
始终是一个定值.求此时![]() 的值及定值
的值及定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
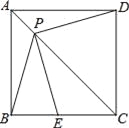
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com