
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§![]() КЭЗДБШР§КЏЪ§
КЭЗДБШР§КЏЪ§![]() ЃЎ
ЃЎ
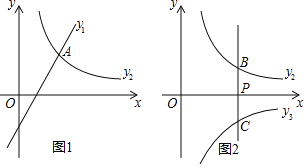
ЃЈ1ЃЉШчЭМ1ЃЌШє![]() ЃЌЧвКЏЪ§
ЃЌЧвКЏЪ§![]() ЁЂ
ЁЂ![]() ЕФЭМЯѓЖМОЙ§Еу
ЕФЭМЯѓЖМОЙ§Еу![]() ЃЎ
ЃЎ
ЂйЧѓ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкжБНгаДГіЕБ![]() ЪБ
ЪБ![]() ЕФЗЖЮЇЃЛ
ЕФЗЖЮЇЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯп
жсЕФЦНааЯп![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() ЃЌгыЗДБШР§КЏЪ§
ЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() ЃЎ
ЃЎ
ЂйШє![]() ЃЌжБЯп
ЃЌжБЯп![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯѓЯрНЛЕу
ЕФЭМЯѓЯрНЛЕу![]() ЃЎЕБЕу
ЃЎЕБЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жаЕФвЛЕуЕНСэЭтСНЕуЕФОрРыЯрЕШЪБЃЌЧѓ
жаЕФвЛЕуЕНСэЭтСНЕуЕФОрРыЯрЕШЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпгыКЏЪ§
жсЕФЦНааЯпгыКЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() ЃЎЕБ
ЃЎЕБ![]() ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪЕЪ§ЪБЃЌЕу
ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪЕЪ§ЪБЃЌЕу![]() ЁЂ
ЁЂ![]() МфЕФОрРыгыЕу
МфЕФОрРыгыЕу![]() ЁЂ
ЁЂ![]() МфЕФОрРыжЎКЭ
МфЕФОрРыжЎКЭ![]() ЪМжеЪЧвЛИіЖЈжЕЃЎЧѓДЫЪБ
ЪМжеЪЧвЛИіЖЈжЕЃЎЧѓДЫЪБ![]() ЕФжЕМАЖЈжЕ
ЕФжЕМАЖЈжЕ![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌ
ЃЌ![]() ЃЛЂк
ЃЛЂк![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() Лђ4ЃЛЂк
Лђ4ЃЛЂк![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйНЋЕу![]() ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНМДПЩЧѓНтЃЌНЋЕу
ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНМДПЩЧѓНтЃЌНЋЕу![]() ЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛЂкгЩЭМЯѓПЩвджБНгПДГіЃЛ
ЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛЂкгЩЭМЯѓПЩвджБНгПДГіЃЛ
ЃЈ2ЃЉЂй![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌгЩ
ЃЌгЩ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЕУЃК
ЕУЃК![]() Лђ0Лђ2ЃЌМДПЩЧѓНтЃЛЂкЕу
Лђ0Лђ2ЃЌМДПЩЧѓНтЃЛЂкЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]()
![]() ЃЌМДПЩЧѓНтЃЎ
ЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЂйНЋЕу![]() ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК
ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК![]() ЃЌ
ЃЌ
НЋЕу![]() ЕФзјБъДњШыЗДБШР§КЏЪ§ЕУЃК
ЕФзјБъДњШыЗДБШР§КЏЪ§ЕУЃК![]() ЃЛ
ЃЛ
ЂкгЩЭМЯѓПЩвдПДГі![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
МДЃК![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
МДЃК![]() Лђ0Лђ2Лђ4ЃЌ
Лђ0Лђ2Лђ4ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гыЬтвтВЛЗћЃЌ
гыЬтвтВЛЗћЃЌ
Еу![]() ВЛФмдк
ВЛФмдк![]() ЕФЯТЗНЃЌМД
ЕФЯТЗНЃЌМД![]() вВВЛДцдкЃЌ
вВВЛДцдкЃЌ![]() ЃЌЙЪ
ЃЌЙЪ![]() ВЛГЩСЂЃЌ
ВЛГЩСЂЃЌ
ЙЪ![]() Лђ4ЃЛ
Лђ4ЃЛ
ЂкЕу![]() ЕФКсзјБъЮЊЃК
ЕФКсзјБъЮЊЃК![]() ЃЌ
ЃЌ
ЕБЕу![]() дкЕу
дкЕу![]() зѓВрЪБЃЌ
зѓВрЪБЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪ§ЪБЃЌ
ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪ§ЪБЃЌ![]() ЪМжеЪЧвЛИіЖЈжЕЃЌ
ЪМжеЪЧвЛИіЖЈжЕЃЌ
ЕБ![]() ЪБЃЌДЫЪБ
ЪБЃЌДЫЪБ![]() ЃЌДгЖј
ЃЌДгЖј![]() ЃЎ
ЃЎ
ЕБЕу![]() дкЕу
дкЕу![]() гвВрЪБЃЌ
гвВрЪБЃЌ
ЭЌРэ![]() ЃЌ
ЃЌ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЃЈВЛКЯЬтвтЩсШЅЃЉ
ЪБЃЌЃЈВЛКЯЬтвтЩсШЅЃЉ
ЙЪ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ


 вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
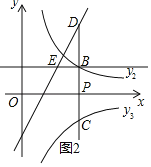
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЖўДЮКЏЪ§
жаЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЌВЂдкЯТЭМжаЛГіЪОвтЭМЃЛ
ЃЈ2ЃЉНЋИУЖўДЮКЏЪ§ЕФЭМЯѓЯђЩЯЦНвЦМИИіЕЅЮЛГЄЖШЃЌПЩЪЙЦНвЦКѓЫљЕУЭМЯѓОЙ§зјБъдЕуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВннЎЪЧдЦФЯЖрЕиЪЂВњЕФвЛжжЫЎЙћЃЌНёФъФГЫЎЙћЯњЪлЕъдкВннЎЯњЪлЭњМОЃЌЪдЯњЪлГЩБОЮЊУПЧЇПЫ![]() дЊЕФВннЎЃЌЙцЖЈЪдЯњЦкМфЯњЪлЕЅМлВЛЕЭгкГЩБОЕЅМлЃЌвВВЛИпгкУПЧЇПЫ
дЊЕФВннЎЃЌЙцЖЈЪдЯњЦкМфЯњЪлЕЅМлВЛЕЭгкГЩБОЕЅМлЃЌвВВЛИпгкУПЧЇПЫ![]() дЊЃЌОЪдЯњЗЂЯжЃЌЯњЪлСП
дЊЃЌОЪдЯњЗЂЯжЃЌЯњЪлСП![]() ЃЈЧЇПЫЃЉгыЯњЪлЕЅМл
ЃЈЧЇПЫЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЌШчЭМЪЧ
ЃЈдЊЃЉЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЌШчЭМЪЧ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЭМЯѓЃЎ
ЕФКЏЪ§ЙиЯЕЭМЯѓЃЎ
![]() Чѓ
Чѓ![]() гы
гы![]() ЕФКЏЪ§НтЮіЪНЃЈвВГЦЙиЯЕЪНЃЉЃЛ
ЕФКЏЪ§НтЮіЪНЃЈвВГЦЙиЯЕЪНЃЉЃЛ
![]() ЩшИУЫЎЙћЯњЪлЕъЪдЯњВннЎЛёЕУЕФРћШѓЮЊ
ЩшИУЫЎЙћЯњЪлЕъЪдЯњВннЎЛёЕУЕФРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
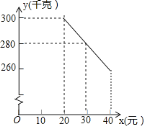
ЁОЬтФПЁПзуЧђШќЪЧЭЌбЇУЧБШНЯЯВЛЖЕФЬхг§БШШќ.ФужЊЕРТ№ЃЌвЛИізуЧђБЛДгЕиУцЯђЩЯЬпГіЃЌЫќОрЕиУцЕФИпЖШ![]() ПЩвдгУЖўДЮКЏЪ§
ПЩвдгУЖўДЮКЏЪ§![]() ПЬЛЃЌЦфжа
ПЬЛЃЌЦфжа![]() БэЪОзуЧђБЛЬпГіКѓОЙ§ЕФЪБМф.
БэЪОзуЧђБЛЬпГіКѓОЙ§ЕФЪБМф.
ЃЈ1ЃЉЗНГЬ![]() ЕФИљЕФЪЕМЪвтвхЪЧ________.
ЕФИљЕФЪЕМЪвтвхЪЧ________.
ЃЈ2ЃЉЮЪОЙ§ЖрГЄЪБМфЃЌзуЧђЕНДяЫќЕФзюИпЕуЃПзюИпЕуЕФИпЖШЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЮвЪаЁАЧрЩНТЬЫЎЁБааЖЏжаЃЌФГЩчЧјМЦЛЎЖдУцЛ§ЮЊ![]() ЕФЧјгђНјааТЬЛЏЃЌОЭЖБъгЩМзЁЂввСНИіЙЄГЬЖгРДЭъГЩЃЎвбжЊМзЖгУПЬьФмЭъГЩТЬЛЏЕФУцЛ§ЪЧввЖгУПЬьФмЭъГЩТЬЛЏУцЛ§ЕФ2БЖЃЌШчЙћСНЖгИїздЖРСЂЭъГЩУцЛ§ЮЊ
ЕФЧјгђНјааТЬЛЏЃЌОЭЖБъгЩМзЁЂввСНИіЙЄГЬЖгРДЭъГЩЃЎвбжЊМзЖгУПЬьФмЭъГЩТЬЛЏЕФУцЛ§ЪЧввЖгУПЬьФмЭъГЩТЬЛЏУцЛ§ЕФ2БЖЃЌШчЙћСНЖгИїздЖРСЂЭъГЩУцЛ§ЮЊ![]() ЧјгђЕФТЬЛЏЪБЃЌМзЖгБШввЖгЩйгУ6ЬьЃЎ
ЧјгђЕФТЬЛЏЪБЃЌМзЖгБШввЖгЩйгУ6ЬьЃЎ
(1)ЧѓМзЁЂввСНЙЄГЬЖгУПЬьИїФмЭъГЩЖрЩйУцЛ§ЕФТЬЛЏЃЛ
(2)ШєМзЖгУПЬьТЬЛЏЗбгУЪЧ1.2ЭђдЊЃЌввЖгУПЬьТЬЛЏЗбгУЮЊ0.5ЭђдЊЃЌЩчЧјвЊЪЙетДЮТЬЛЏЕФзмЗбгУВЛГЌЙ§40ЭђдЊЃЌдђжСЩйгІАВХХввЙЄГЬЖгТЬЛЏЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬ
(1)(xЉ2)2=9.
(2)3x2Љ1=2x.
(3)x2+4x+1=0.
(4)(x+1)2Љ6(x+1)+5=0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
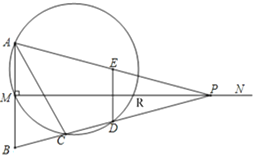
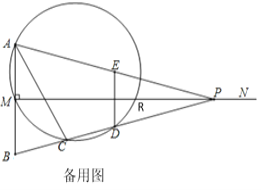
ЁОЬтФПЁПШчЭМЃЌвбжЊЯпЖЮABЃН2ЃЌMNЁЭABгкЕуMЃЌЧвAMЃНBMЃЌPЪЧЩфЯпMNЩЯвЛЖЏЕуЃЌEЃЌDЗжБ№ЪЧPAЃЌPBЕФжаЕуЃЌЙ§ЕуAЃЌMЃЌDЕФдВгыBPЕФСэвЛНЛЕуC(ЕуCдкЯпЖЮBDЩЯ)ЃЌгыMNЕФСэвЛИіНЛЕуRЃЌСЌНсACЃЌDEЃЎ
(1)ЕБЁЯAPBЃН28ЁуЪБЃЌЧѓЁЯBЕФЖШЪ§КЭЛЁCMЕФЖШЪ§ЃЎ
(2)ЧѓжЄЃКACЃНABЃЎ
(3)ШєMP=4ЃЌЕуPЮЊЩфЯпMNЩЯЕФвЛИіЖЏЕуЃЌ
ЂйЧѓMRЕФжЕ
ЂкдкЕуPЕФдЫЖЏЙ§ГЬжаЃЌШЁЫФБпаЮACDEвЛБпЕФСНЖЫЕуКЭЯпЖЮMPЩЯвЛЕуQЃЌШєвдетШ§ЕуЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌЧвQЮЊШёНЧЖЅЕуЃЌЧѓДЫЪБЫљгаТњзуЬѕМўЕФMQЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЧђЪвгаШ§жжЦЗХЦЕФ![]() ИіЦЙХвЧђЃЌМлИёЪЧ7ЃЌ8ЃЌ9ЃЈЕЅЮЛЃКдЊЃЉШ§жжЃЎДгжаЫцЛњФУГівЛИіЧђЃЌвбжЊ
ИіЦЙХвЧђЃЌМлИёЪЧ7ЃЌ8ЃЌ9ЃЈЕЅЮЛЃКдЊЃЉШ§жжЃЎДгжаЫцЛњФУГівЛИіЧђЃЌвбжЊ![]() ЃЈвЛДЮФУЕН
ЃЈвЛДЮФУЕН![]() дЊЧђЃЉ
дЊЧђЃЉ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓет![]() ИіЧђМлИёЕФжкЪ§ЃЛ
ИіЧђМлИёЕФжкЪ§ЃЛ
ЃЈ2ЃЉШєМззщвбФУзпвЛИі![]() дЊЧђбЕСЗЃЌввзщзМБИДгЪЃгр
дЊЧђбЕСЗЃЌввзщзМБИДгЪЃгр![]() ИіЧђжаЫцЛњФУвЛИібЕСЗЃЎ
ИіЧђжаЫцЛњФУвЛИібЕСЗЃЎ
ЂйЫљЪЃЕФ![]() ИіЧђМлИёЕФжаЮЛЪ§гыдРД
ИіЧђМлИёЕФжаЮЛЪ§гыдРД![]() ИіЧђМлИёЕФжаЮЛЪ§ЪЧЗёЯрЭЌЃПВЂМђвЊЫЕУїРэгЩЃЛ
ИіЧђМлИёЕФжаЮЛЪ§ЪЧЗёЯрЭЌЃПВЂМђвЊЫЕУїРэгЩЃЛ
ЂкввзщЯШЫцЛњФУГівЛИіЧђКѓЗХЛиЃЌжЎКѓгжЫцЛњФУвЛИіЃЌгУСаБэЗЈЃЈШчЭМЃЉЧѓввзщСНДЮЖМФУЕН8дЊЧђЕФИХТЪЃЎ
гжФУ ЯШФУ | |||
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
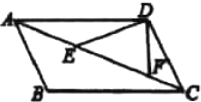
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯСНЕуЃЌ
ЩЯСНЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФДѓаЁЮЊ______.
ЕФДѓаЁЮЊ______.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com