
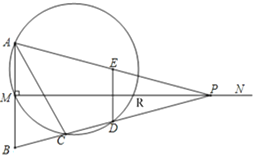
،¾جâؤ؟،؟بçح¼£¬زرضھدك¶خAB£½2£¬MN،حABسعµمM£¬ازAM£½BM£¬PتاةندكMNةدز»¶¯µم£¬E£¬D·ض±ًتاPA£¬PBµؤضذµم£¬¹µمA£¬M£¬Dµؤش²سëBPµؤءيز»½»µمC(µمCشعدك¶خBDةد)£¬سëMNµؤءيز»¸ِ½»µمR£¬ء¬½لAC£¬DE£®
(1)µ±،دAPB£½28،مت±£¬اَ،دBµؤ¶بت؛ح»،CMµؤ¶بت£®
(2)اَض¤£؛AC£½AB£®
(3)بôMP=4£¬µمPخھةندكMNةدµؤز»¸ِ¶¯µم£¬
¢ظاَMRµؤضµ
¢عشعµمPµؤشث¶¯¹³جضذ£¬ب،ثؤ±كذخACDEز»±كµؤء½¶ثµم؛حدك¶خMPةدز»µمQ£¬بôزشصâبµمخھ¶¥µمµؤب½اذختاض±½اب½اذخ£¬ازQخھبٌ½ا¶¥µم£¬اَ´ثت±ثùسذآْ×مجُ¼µؤMQµؤضµ£®
،¾´ً°¸،؟(1)،دB=76،م£¬![]() =56،م£»(2)ض¤أ÷¼û½âخِ£»(3)¢ظMR=
=56،م£»(2)ض¤أ÷¼û½âخِ£»(3)¢ظMR=![]() £»¢عMQµؤضµخھ
£»¢عMQµؤضµخھ![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() .
.
،¾½âخِ،؟
£¨1£©ء¬½سMD£¬½ل؛د´¹ض±ئ½·ضدكµؤذشضتسëµبرüب½اذخذشضت½ل؛دب½اذخؤع½ا؛ح¶¨ہي£¬ضذخ»دك¶¨ہياَ½â¼´؟ة£»
£¨2£©اَض¤،دABC=،دACB¼´؟ة£»
£¨3£©¢ظء¬½سCR£¬AR£¬½ل؛د¹´¹ة¶¨ہياَ½â¼´؟ة£»¢ع·ضخھµ±،دACQ=90،مت±£»µ±،دQCD=90،مت±£»µ±،دQDC=90،مت±£»µ±،دAEQ=90،مت±£¬·ضہàجضآغ¼´؟ة£®
½â£؛(1)،كMN،حAB£¬AM=BM£¬
،àPA=PB£¬
،à،دPAB=،دB£¬
،ك،دAPB=28،م£¬
،à،دB=76،م£¬
بçح¼1£¬ء¬½سMD£¬
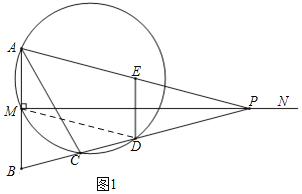
،كMDخھ،÷PABµؤضذخ»دك£¬
،àMD،خAP£¬
،à،دMDB=،دAPB=28،م£¬
،à![]() =2،دMDB=56،م£»
=2،دMDB=56،م£»
(2)،ك،دBAC=،دMDC=،دAPB£¬
سض،ك،دBAP=180،م©پ،دAPB©پ،دB£¬،دACB=180،م©پ،دBAC©پ،دB£¬
،à،دBAP=،دACB£¬
،ك،دBAP=،دB£¬
،à،دACB=،دB£¬
،àAC=AB£»
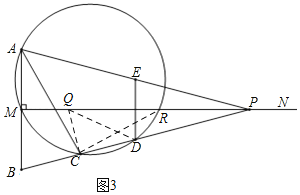
(3)¢ظبçح¼2£¬¼اMPسëش²µؤءيز»¸ِ½»µمخھR£¬

،كMDتاRt،÷MBPµؤضذدك£¬
،àDM=DP£¬
،à،دDPM=،دDMP=،دRCD£¬
،àRC=RP£¬
،ك،دACR=،دAMR=90،م£¬
،àAM2+MR2=AR2=AC2+CR2£¬
،à12+MR2=22+PR2£¬
،à12+(4©پPR)2=22+PR2£¬
،àPR=![]() £¬
£¬
،àMR=![]() £¬
£¬
¢ع¢ٌ£®µ±،دACQ=90،مت±£¬AQخھش²µؤض±¾¶£¬
،àQسëRضط؛د£¬
،àMQ=MR=![]() £»
£»
¢ٍ£®بçح¼3£¬µ±،دQCD=90،مت±£¬
شعRt،÷QCPضذ£¬PQ=2PR=![]() £¬
£¬
،àMQ=![]() £»
£»
¢َ£®بçح¼4£¬µ±،دQDC=90،مت±£¬

،كBM=1£¬MP=4£¬
،àBP=![]() £¬
£¬
،àDP=![]() BP=
BP=![]() £¬
£¬
،كcos،دMPB=![]()
![]() £¬
£¬
،àPQ=![]() £¬
£¬
،àMQ=![]() £»
£»
¢ô£®بçح¼5£¬µ±،دAEQ=90،مت±£¬
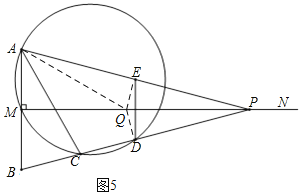
سة¶ش³ئذش؟ةµأ،دAEQ=،دBDQ=90،م£¬
،àMQ=![]() £»
£»
×غةدثùتِ£¬MQµؤضµخھ![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() .
.



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
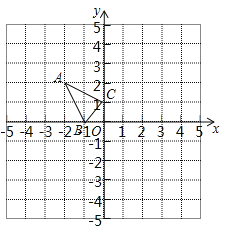
،¾جâؤ؟،؟بçح¼1£¬ئ½أوض±½ا×ّ±êدµضذ£¬B،¢Cء½µمµؤ×ّ±ê·ض±ًخھB£¨0£¬3£©؛حC£¨0£¬©پ![]() £©£¬µمAشعxضلص°ëضلةد£¬ازآْ×م،دBAO£½30،م£®
£©£¬µمAشعxضلص°ëضلةد£¬ازآْ×م،دBAO£½30،م£®
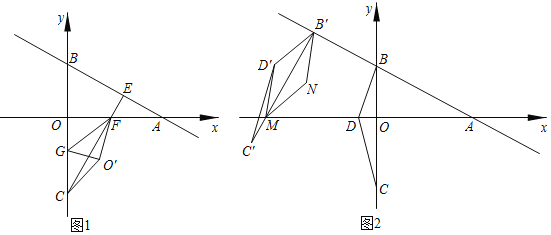
£¨1£©¹µمC×÷CE،حABسعµمE£¬½»AOسعµمF£¬µمGخھدك¶خOCةدز»¶¯µم£¬ء¬½سGF£¬½«،÷OFGرطFG·صغت¹µمOآنشعئ½أوؤعµؤµمO،ن´¦£¬ء¬½سO،نC£¬اَدك¶خOFµؤ³¤زش¼°دك¶خO،نCµؤ×îذ،ضµ£»
£¨2£©بçح¼2£¬µمDµؤ×ّ±êخھD£¨©پ1£¬0£©£¬½«،÷BDCبئµمBث³ت±صëذ×ھ£¬ت¹µأBC،حABسعµمB£¬½«ذ×ھ؛َµؤ،÷BDCرطض±دكABئ½زئ£¬ئ½زئضذµؤ،÷BDC¼اخھ،÷B،نD،نC،ن£¬ةèض±دكB،نC،نسëxضل½»سعµمM£¬Nخھئ½أوؤعبخزâز»µم£¬µ±زشB،ن،¢D،ن،¢M،¢Nخھ¶¥µمµؤثؤ±كذختاءâذخت±£¬اَµمMµؤ×ّ±ê£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬![]() تا
تا![]() µؤاذدك£¬اذµمخھ
µؤاذدك£¬اذµمخھ![]() £¬
£¬![]() تا
تا![]() µؤض±¾¶£¬ء¬½س
µؤض±¾¶£¬ء¬½س![]() ½»
½»![]() سع
سع![]() £®¹
£®¹![]() µم×÷
µم×÷![]() سعµم
سعµم![]() £¬½»
£¬½»![]() سع
سع![]() £¬ء¬½س
£¬ء¬½س![]() £¬
£¬![]() £®
£®
(1)اَض¤£؛![]() تا
تا![]() µؤاذدك£»
µؤاذدك£»
(2)اَض¤£؛![]() خھ
خھ![]() µؤؤعذؤ£»
µؤؤعذؤ£»
(3)بô![]() £¬
£¬![]() £¬اَ
£¬اَ![]() µؤ³¤£®
µؤ³¤£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھز»´خ؛¯ت![]() ؛ح·´±بہ؛¯ت
؛ح·´±بہ؛¯ت![]() £®
£®
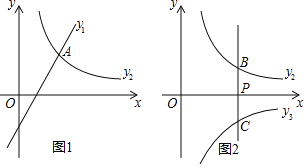
£¨1£©بçح¼1£¬بô![]() £¬از؛¯ت
£¬از؛¯ت![]() ،¢
،¢![]() µؤح¼دَ¶¼¾¹µم
µؤح¼دَ¶¼¾¹µم![]() £®
£®
¢ظاَ![]() £¬
£¬![]() µؤضµ£»
µؤضµ£»
¢عض±½سذ´³ِµ±![]() ت±
ت±![]() µؤ·¶خ§£»
µؤ·¶خ§£»
£¨2£©بçح¼2£¬¹µم![]() ×÷
×÷![]() ضلµؤئ½ذذدك
ضلµؤئ½ذذدك![]() سë؛¯ت
سë؛¯ت![]() µؤح¼دَدཻسعµم
µؤح¼دَدཻسعµم![]() £¬سë·´±بہ؛¯ت
£¬سë·´±بہ؛¯ت![]() µؤح¼دَدཻسعµم
µؤح¼دَدཻسعµم![]() £®
£®
¢ظبô![]() £¬ض±دك
£¬ض±دك![]() سë؛¯ت
سë؛¯ت![]() µؤح¼دَدཻµم
µؤح¼دَدཻµم![]() £®µ±µم
£®µ±µم![]() ،¢
،¢![]() ،¢
،¢![]() ضذµؤز»µمµ½ءيحâء½µمµؤ¾àہëدàµبت±£¬اَ
ضذµؤز»µمµ½ءيحâء½µمµؤ¾àہëدàµبت±£¬اَ![]() µؤضµ£»
µؤضµ£»
¢ع¹µم![]() ×÷
×÷![]() ضلµؤئ½ذذدكسë؛¯ت
ضلµؤئ½ذذدكسë؛¯ت![]() µؤح¼دَدཻسعµم
µؤح¼دَدཻسعµم![]() £®µ±
£®µ±![]() µؤضµب،²»´َسع1µؤبخزâتµتت±£¬µم
µؤضµب،²»´َسع1µؤبخزâتµتت±£¬µم![]() ،¢
،¢![]() ¼نµؤ¾àہëسëµم
¼نµؤ¾àہëسëµم![]() ،¢
،¢![]() ¼نµؤ¾àہëض®؛ح
¼نµؤ¾àہëض®؛ح![]() ت¼ضصتاز»¸ِ¶¨ضµ£®اَ´ثت±
ت¼ضصتاز»¸ِ¶¨ضµ£®اَ´ثت±![]() µؤضµ¼°¶¨ضµ
µؤضµ¼°¶¨ضµ![]() £®
£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ£¬،÷ ABC شعض±½ا×ّ±êدµؤع£¬ب¸ِ¶¥µمµؤ×ّ±ê·ض±ًخھA£¨-2£¬2£©،¢B£¨-1£¬0£©،¢C£¨0£¬1£©£¨ص·½ذخحّ¸ٌضذأ؟¸ِذ،ص·½ذخµؤ±ك³¤تاز»¸ِµ¥خ»³¤¶ب£©.
(1)»³ِ،÷ ABC ¹طسع y ضلµؤضل¶ش³ئح¼ذخ،÷ A1B1C1£»
(2)ز»µم O خھخ»ؤâضذذؤ£¬شعحّ¸ٌؤع»³ِثùسذ·û؛دجُ¼µؤ،÷ A2B2C2£¬ت¹،÷ A2B2C2 سë،÷ A1B1C1 خ»ؤ⣬ازخ»ؤâ±بخھ 2:1£»
(3) ،÷ A1B1C1 سë،÷ A2B2C2 µؤأو»±بخھ .
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعثؤ±كذخ ABCD ضذ£¬¶ش½ادك AC،¢BD دཻسعµم O£¬¹µم O µؤء½جُض±دك·ض±ً½»±ك AB،¢CD،¢AD،¢BC سعµم E،¢F،¢G،¢H£®
£¨¸ذضھ£©بçح¼¢ظ£¬بôثؤ±كذخ ABCD تاص·½ذخ£¬از AG£½BE£½CH£½DF£¬شٍ S ثؤ±كذخAEOG£½ S ص·½ذخ ABCD£»
£¨حطص¹£©بçح¼¢ع£¬بôثؤ±كذخ ABCD تا¾طذخ£¬از S ثؤ±كذخ AEOG£½![]() S ¾طذخ ABCD£¬ةè AB£½a£¬ AD£½b£¬BE£½m£¬اَ AG µؤ³¤£¨سأ؛¬ a،¢b،¢m µؤ´ْتت½±يت¾£©£»
S ¾طذخ ABCD£¬ةè AB£½a£¬ AD£½b£¬BE£½m£¬اَ AG µؤ³¤£¨سأ؛¬ a،¢b،¢m µؤ´ْتت½±يت¾£©£»
£¨ج½¾؟£©بçح¼¢غ£¬بôثؤ±كذخ ABCD تائ½ذذثؤ±كذخ£¬از AB£½3£¬AD£½5£¬BE£½1£¬ تشب·¶¨ F،¢G،¢H µؤخ»ضأ£¬ت¹ض±دك EF،¢GH °رثؤ±كذخ ABCD µؤأو»ثؤµب·ض£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟2017ؤêضذاï½عہ´ئع¼ن£¬ؤ³³¬تذزشأ؟؛ذ80شھµؤ¼غ¸ٌ¹؛½ّءث1000؛ذشآ±£¬µعز»ضـزشأ؟؛ذ168شھµؤ¼غ¸ٌدْتغءث300؛ذ£¬µع¶ضـبç¹ûµ¥¼غ²»±ن£¬ش¤¼ئبش؟ةتغ³ِ300؛ذ£¬¸أ³¬تذ¾ہيخھءثشِ¼سدْء؟£¬¾ِ¶¨½µ¼غ£¬¾فµ÷²é£¬µ¥¼غأ؟½µµح1شھ£¬؟ة¶àتغ³ِ10؛ذ£¬µ«×îµحأ؟؛ذزھس®ہû30شھ£¬µع¶ضـ½لتّ؛َ£¬¸أ³¬تذ½«¶شت£سàµؤشآ±ز»´خذشإâا®ث¦آô£¬´ثت±¼غ¸ٌخھ70شھ/؛ذ£®
£¨1£©بôةèµع¶ضـµ¥¼غ½µµحxشھ£¬شٍµع¶ضـµؤµ¥¼غتا ______ £¬دْء؟تا ______ £»
£¨2£©¾ء½ضـ؛َ»¹ت£سàشآ± ______ ؛ذ£»
£¨3£©بô¸أ³¬تذدëح¨¹دْتغصâإْشآ±»ٌہû51360شھ£¬ؤاأ´µع¶ضـµؤµ¥¼غس¦تا¶àشھ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
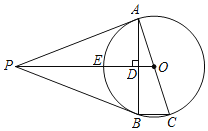
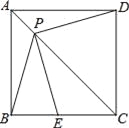
،¾جâؤ؟،؟بçح¼£¬Pتاص·½ذخABCD¶ش½ادكACةدز»µم£¬µمEشعBCةد£¬ازPE=PB£®
£¨1£©اَض¤£؛PE=PD£»
£¨2£©ء¬½سDE£¬تشإذ¶د،دPEDµؤ¶بت£¬²¢ض¤أ÷ؤمµؤ½لآغ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شع![]() ضذ£¬ذ±±كACµؤضذµمM¹طسعBCµؤ¶ش³ئµمO£¬½«،÷ABCبئµمOث³ت±صëذ×ھضء،÷DCE£¬ء¬½سBD£¬BE£¬بçح¼ثùت¾.
ضذ£¬ذ±±كACµؤضذµمM¹طسعBCµؤ¶ش³ئµمO£¬½«،÷ABCبئµمOث³ت±صëذ×ھضء،÷DCE£¬ء¬½سBD£¬BE£¬بçح¼ثùت¾.
(1)شع¢ظ![]() £¬¢ع
£¬¢ع![]() £¬¢غ
£¬¢غ![]() ضذ£¬µبسعذ×ھ½اµؤتا £¨جî³ِآْ×مجُ¼µؤ½اµؤذٍ؛إ£©£»
ضذ£¬µبسعذ×ھ½اµؤتا £¨جî³ِآْ×مجُ¼µؤ½اµؤذٍ؛إ£©£»
(2)بô![]() اَ
اَ![]() µؤ´َذ،£¨سأ؛¬
µؤ´َذ،£¨سأ؛¬![]() µؤت½×س±يت¾£©£»
µؤت½×س±يت¾£©£»
(3)µمNتاBDµؤضذµم£¬ء¬½سMN£¬سأµبت½±يت¾دك¶خMNسëBEض®¼نµؤتء؟¹طدµ£¬²¢ض¤أ÷.

²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com