
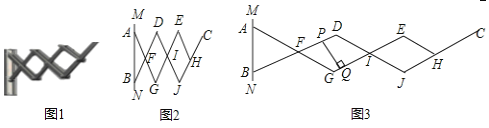
【题目】如图1,是一个三节段式伸缩晾衣架,如图2,是其衣架侧面示意图.MN为衣架的墙体固定端,A为固定支点,B为滑动支点,四边形DFGI和四边形EIJH是菱形,且AF=BF=CH=DF=EH.点B在AN上滑动时,衣架外延钢体发生角度形变,其外延长度(点A和点C间的距离)也随之变化,形成衣架伸缩效果.伸缩衣架为初始状态时,衣架外延长度为42cm.当点B向点A移动8cm时,外延长度为90cm.如图3,当外延长度为120cm时,则BD和GE的间距PQ长为______________cm.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=土9,因为2m2+n2>0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整休,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值.
(2)已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于点A,点B,抛物线
与x轴,y轴分别交于点A,点B,抛物线![]() 经过A,B与点
经过A,B与点![]() .
.
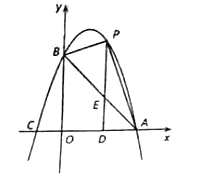
(1)求抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线,垂足为D,交线段AB于点E.设点P的横坐标为m.
①求![]() 的面积y关于m的函数关系式,当m为何值时,y有最大值,最大值是多少?
的面积y关于m的函数关系式,当m为何值时,y有最大值,最大值是多少?
②若点E是垂线段PD的三等分点,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
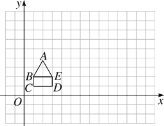
【题目】已知:如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其点B,C,D的坐标分别为(1,2),(1,1),(3,1).
(1)直接写出E点和A点的坐标;
(2)试以点B为位似中心,作出位似图形A1B1C1D1E1,使所作的图形与原图形的位似比为3∶1;
(3)直接写出图形A1B1C1D1E1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,![]() ,
,![]() ,AD=CD,对角线AC,BD相交于点O,且BD平分∠ABC,过点A作
,AD=CD,对角线AC,BD相交于点O,且BD平分∠ABC,过点A作![]() ,垂足为H.
,垂足为H.
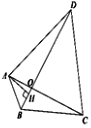
(1)求证:![]() ;
;
(2)判断线段BH,DH,BC之间的数量关系;并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接BD,当![]() 时,求△DNB的面积;
时,求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,直接写出此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
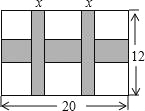
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com