
 如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).分析 (1)当边FG恰好经过点C时,由∠CFB=60°得BF=3-t,在Rt△CBF中,根据三角函数求得t的值;
(2)根据运动的时间为t不同的取值范围,求等边△EFG和矩形ABCD重叠部分的面积为S的值,当0≤t<1时,重叠部分是直角梯形,面积S等于梯形的面积,
当1≤t<3时,重叠部分是S梯形MKFE-S△QBF,当3≤t<4时,重叠部分是S梯形MKFE,当4≤t<6时,重叠部分是正三角形的面积;
(3)当AH=AO=3时,AM=$\frac{1}{2}$AH=$\frac{3}{2}$,在Rt△AME中,由cos∠MAE=$\frac{AM}{AE}$即cos30°=$\frac{\frac{3}{2}}{AE}$,得AE=$\sqrt{3}$,即3-t=$\sqrt{3}$或t-3=$\sqrt{3}$,求出t=3-$\sqrt{3}$或t=3+$\sqrt{3}$;
当AH=HO时,∠HOA=∠HAO=30°,又因为∠HEO=60°得到∠EHO=90°EO=2HE=2AE,再由AE+2AE=3,求出AE=1,即3-t=1或t-3=1,求出t=2或t=4;
当OH=OA=时∠HOB=∠OAH=30°,所以∠HOB=60°=∠HEB,得到点E和点O重合,从而求出t的值
解答 解:如图1(1),当边FG恰好经过点C时,
∵∠CFB=60°,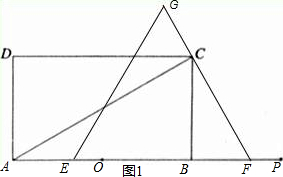
∴BF=3-t,
在Rt△CBF中,
∵BC=2$\sqrt{3}$,tan∠CFB=$\frac{BC}{BF}$,
∴tan60=$\frac{2\sqrt{3}}{BF}$,
解得BF=2,即3-t=2,
∴t=1,
当边FG恰好经过点C时,t=1;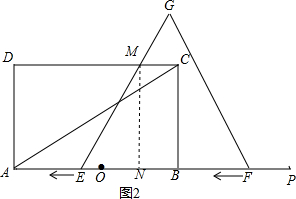
(2)如图2,过点M作MN⊥AB于N,
当0≤t<1时,
∵tan60°=$\frac{MN}{EN}$=$\frac{2\sqrt{7}}{EN}$=$\sqrt{3}$,
∴EN=2,
∵EB=3+t,NB=3+t-2=1+t,
∴MC=1+t,
∴S=$\frac{1}{2}$(MC+EB)•BC=2$\sqrt{3}$t+4$\sqrt{3}$;
如图3,当1≤t<3时,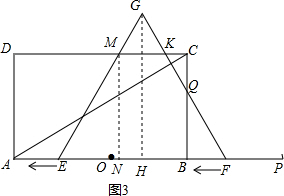
∵MN=2$\sqrt{3}$ EF=OP=6,
GH=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴$\frac{MK}{EF}$=$\frac{GH-MN}{GH}$,
∴MK=2,
∵EB=3+t,BF=3-t,BQ=$\sqrt{3}$t-$\sqrt{3}$,
∴S=S梯形MKFE-S△QBF=-$\frac{\sqrt{3}}{2}$t2+3$\sqrt{3}$t+$\frac{7\sqrt{3}}{2}$;
如图4,当3≤t<4时,
∵MN=2$\sqrt{3}$,EF=6-2(t-3)=12-2t,
∴GH=(12-2t)×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$-$\sqrt{3}$t,∴$\frac{MK}{EF}$=$\frac{GH-MN}{GH}$,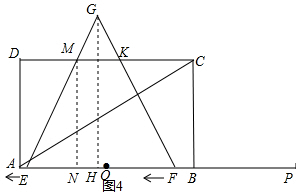
∴MK=8-2t,
∴S=-4$\sqrt{3}$t+20$\sqrt{3}$;
当4≤t<6时,
∵EF=12-2t,
∴高为:EFsin60°=$\frac{\sqrt{3}}{2}$EF,
∴S=$\sqrt{3}$t2-12$\sqrt{3}$t+36$\sqrt{3}$;
(3)存在.
在Rt△ABC中,tan$∠CAB=\frac{BC}{AB}=\frac{\sqrt{3}}{3}$,∴∠CAB=30°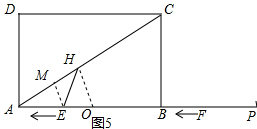
∵$∠HEO\$=60°,
∴∠HAE=∠AHE 30°,
∴AE=HE=3-t或t-3,
如图5,当AH=AO=3时,
过点E作EM⊥AH与M,
则AM=$\frac{1}{2}$AH=$\frac{3}{2}$,
在Rt△AME中,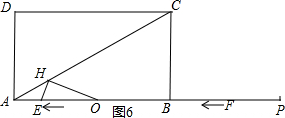
cos∠MAE=$\frac{AM}{AE}$即cos30°=$\frac{\frac{3}{2}}{AE}$,
∴AE=$\sqrt{3}$,
即3-t=$\sqrt{3}$或t-3=$\sqrt{3}$;
∴t=3-$\sqrt{3}$或t=3+$\sqrt{3}$;
如图6,当AH=HO时,∠HOA=∠HAO=30°,
∵∠HEO=60°,
∴∠EHO=90°,EO=2HE=2AE,
∵AE+2AE=3,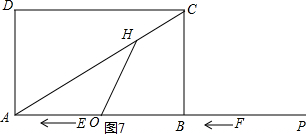
∴AE=1,即3-t=1或t-3=1,
∴t=2或t=4;
如图7,当OH=OA=时,
∠HOB=∠OAH=30°,
∴∠HOB=60°=∠HEB,
∴点E和点O重合,
∴AE=AO=3,
当E刚开始时,3-t=3,
当E返回时t-3=3,
∴t=0,t=6(舍去),
综上所述当t=3-$\sqrt{3}$,t=3+$\sqrt{3}$,t=2,t=4,t=0时,△AOH是等腰三角形.
点评 此题主要考查了 平行四边形的性质、平行四边形的判定、矩形、矩形的性质、矩形的判定、菱形、菱形的性质、菱形的判定 等知识点


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
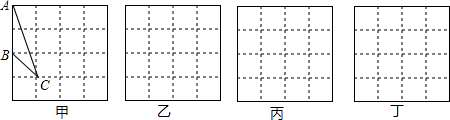
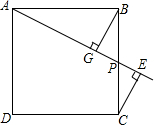 P是边长为4的正方形ABCD的边BC上任一点,过B作BG⊥AP于G,过C作CE⊥AP于E,连BE.
P是边长为4的正方形ABCD的边BC上任一点,过B作BG⊥AP于G,过C作CE⊥AP于E,连BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com