
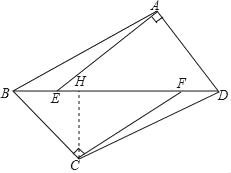
【题目】已知:如图,在四边形ABCD中,过A,C分别作AD和BC的垂线,交对角线BD于点E,F,AE=CF,BE=DF.
(1)求证:四边形ABCD是平行四边形;
(2)若BC=4,∠CBD=45°,且E,F是BD的三等分点,求四边形ABCD的面积.(直接写出结论即可)

【答案】(1)证明见解析;(2)24.
【解析】
(1)证Rt△ADE≌Rt△CBF(HL),得AD=BC,∠ADE=∠CBF,AD∥BC,故四边形ABCD是平行四边形;(2)过C作CH⊥BD于H,证△CBF是等腰直角三角形,得BF=![]() BC=4
BC=4![]() ,CH=
,CH=![]() BC=2
BC=2![]() ,得BD=6
,得BD=6![]() ,故四边形ABCD的面积=BDCH.
,故四边形ABCD的面积=BDCH.
(1)证明:∵AE⊥AD,CF⊥BC,
∴∠DAE=∠BCF=90°,
∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
在Rt△ADE与Rt△CBF中,
![]()
∴Rt△ADE≌Rt△CBF(HL),
∴AD=BC,∠ADE=∠CBF,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:过C作CH⊥BD于H,
∵∠CBD=45°,
∴△CBF是等腰直角三角形,
∴BF=![]() BC=4
BC=4![]() ,CH=
,CH=![]() BC=2
BC=2![]() ,
,
∵E,F是BD的三等分点,
∴BD=6![]() ,
,
∴四边形ABCD的面积=BDCH=24.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E、 F为AB上的一点,CF⊥AD于H,下列判断正确的有( )

A.AD是△ABE的角平分线B.BE是△ABD边AD上的中线
C.AH为△ABC的角平分线D.CH为△ACD边AD上的高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
图书类别 | 画记 | 人数 | 百分比 | ||
文学类 | |||||
艺体类 | 正 | 5 | |||
科普类 | |||||
其他 | 正正 | 14 | |||
合计 | a | 100% |
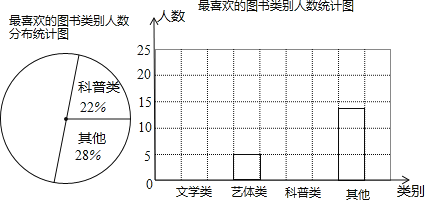
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量![]() 为________;
为________;
(2)在扇形统计图中,“艺体类”所在的扇形圆心角应等于_________度;
(3)补全条形统计图;
(4)已知该校有![]() 名学生,估计全校最喜欢文学类图书的学生有________人.
名学生,估计全校最喜欢文学类图书的学生有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚做游戏一个不透明的布袋里装有4个大小、质地均相同的乒乓球,球上分别标有数字1,2,3,4,随机从布袋中摸出一个乒乓球,记下数字后放回布袋里,再随机从布袋中摸出一个乒乓球,若这两个乒乓球上的数字之和能被4整除则小明赢;若两个乒乓球上的数字之和能被5整除则小刚赢;这个一个对游戏双方公平的游戏吗?请列表格或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)
(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由
(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;
(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com