
【题目】如图①,在等腰Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D.点P为线段CD上一点(不与端点C、D重合),PE⊥PA,PE与BC的延长线交于点E,与AC交于点F,连接AE、AP、BP.
(1)求证:AP=BP;
(2)求∠EAP的度数;
(3)探究线段EC、PD之间的数量关系,并证明.
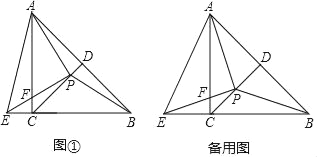
【答案】(1)见解析;(2)45°;(3)EC=![]() PD,理由见解析
PD,理由见解析
【解析】
(1)根据等腰直角三角形的性质可得CD是AB的垂直平分线,根据垂直平分线的性质可得AP=BP;
(2)由∠ACE=∠APE=90°,可得点A,点P,点C,点E四点共圆,可得∠AEP=∠ACD=45°,即可求∠EAP的度数;
(3)过点E作EH⊥CD于点H,根据“AAS”可证△APD≌△PEH,可得EH=PD,根据勾股定理可求EC=![]() EH,即可得EC=
EH,即可得EC=![]() PD.
PD.
证明:(1)∵∠ACB=90°,AC=BC,CD平分∠ACB,
∴CD⊥AB,AD=BD,∠ACD=∠BCD=∠CAD=∠DBC=45°,
∴CD是AB的垂直平分线
∴AP=BP,
(2)∵∠ACE=∠APE=90°,
∴点A,点P,点C,点E四点共圆,
∴∠AEP=∠ACD=45°,且AP⊥EP,
∴∠EAP=45°
(3)EC=![]() PD,理由如下:
PD,理由如下:
如图,过点E作EH⊥CD于点H,
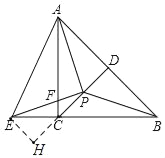
∵∠EAP=∠AEP=45°,
∴AP=PE,
∵∠APE=90°=∠ADP
∴∠APD+∠PAD=90°,∠APD+∠EPH=90°,
∴∠PAD=∠EPH,且AP=PE,∠EHP=∠ADP=90°
∴△APD≌△PEH(AAS)
∴EH=PD,
∵∠ECH=∠DCB=45°,EH⊥CD
∴∠HEC=∠HCE=45°
∴EH=CH
在Rt△ECH中,EC=![]() =
=![]() EH
EH
∴EC=![]() PD.
PD.


科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则AG+GE=______m,由此可得小聪行走的路程为_______m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在直角坐标系内的位置如图所示
(1)分别写出点A,C的坐标:A: ,C: ;
(2)△ABC的周长为 ,面积为 ;
(3)请在这个坐标系内画出△A1B1C1与△ABC关于x轴对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4. 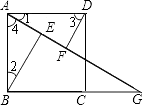
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
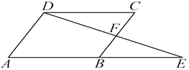
A. ∠E=∠CDF B. BE=CD C. ∠ADE=∠BFE D. BE=2CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
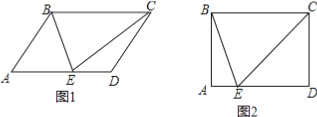
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【试题背景】已知:l ∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3 , 且d1 =d3 = 1,d2 = 2 .我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.
(1)【探究1】如图1,正方形ABCD为“格线四边形”,BE![]() L于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.
L于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.
(2)【探究2】矩形ABCD为“格线四边形”,其长 :宽 = 2 :1 ,求矩形ABCD的宽
(3)【探究3】如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形, ![]() 于点E, ∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC=DF.
于点E, ∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC=DF.
(4)【拓 展】如图3,l ∥k,等边三角形ABC的顶点A、B分别落在直线l、k上, ![]() 于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE,
于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE, ![]() 于点H.
于点H.
猜想:DH在什么范围内,BC∥DE?直接写出结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com