
【题目】(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),
上一动点(不与B,C重合),
求证:![]() PA=PB+PC.
PA=PB+PC.

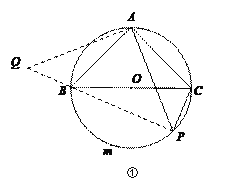
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
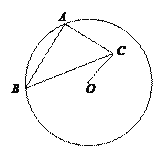
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.

(3)拓展延伸
如图,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
【答案】(1)证明见解析(2)3![]() -2(3)
-2(3)![]()
【解析】
分析: (1)将△PAC绕着点A顺时针旋转90°至△QAB(如图①),只要证明△APQ是等腰直角三角形即可解决问题,(2)如图②中,连接OA,将△OAC绕点O顺时针旋转90°至△QAB,连接OB,OQ,在△BOQ中,利用三边关系定理即可解决问题,
(3)如图③构造相似三角形即可解决问题,作AQ⊥OA,使得AQ=![]() OA,连接OQ,BQ,OB,
OA,连接OQ,BQ,OB,
由△QAB∽△OAC,推出BQ=![]() OC,当BQ最小时,OC最小.
OC,当BQ最小时,OC最小.
详解:(1)证明:∵BC是直径,
∴∠BAC=90°,
∵AB=AC,
∴∠ACB=∠ABC=45°,
由旋转可得∠QBA=∠PCA,∠ACB=∠APB=45°,PC=QB,
∵∠PCA+∠PBA=180°,
∴∠QBA+∠PBA=180°,
∴Q,B,P三点共线,
∴∠QAB+∠BAP=∠BAP+∠PAC=90°
∴QP2=AP2+AQ2=2AP2
∴QP=![]() AP=QB+BP=PC+PB,
AP=QB+BP=PC+PB,
∴![]() AP=PC+PB,
AP=PC+PB,
(2)解:连接OA,将△OAC绕点O顺时针旋转90°至△QAB,连接OB,OQ,
∵AB⊥AC,
∴∠BAC=90°.
由旋转可得 QB=OC.AQ=OA.∠QAB=∠OAC.
∴∠QAB+∠BAO=∠BAO+∠OAC=90°.
∴在Rt△OAQ中.OQ=3![]() ,AO=3,
,AO=3,
∴在△OQB中,BQ≥OQ-OB=3![]() -3,
-3,
即OC最小值是3![]() -3,
-3,
(3)如图中,作AQ⊥OA,使得AQ=![]() OA,连接OQ,BQ,OB,
OA,连接OQ,BQ,OB,
∵∠QAO=∠BAC=90°,
∠QAB=∠OAC,
∵![]() ,
,
∴△QAB∽△OAC,
∴BQ=![]() OC,
OC,
当BQ最小时,OC最小,易知OA=3,AQ=4,OQ=5,BQ≥OQ-OB,
∴OQ≥2,
∴BQ的最小值为2,
∴OC的最小值为![]() ,故答案为
,故答案为![]() .
.
点睛: 本题考查圆综合题,全等三角形的判定和性质,相似三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理,三角形的三边关系等知识,解题的关键是学会利用旋转法添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:
【题目】某校为了了解本校七年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对七年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中中度近视人数是不近视与重度近视人数之和的一半.
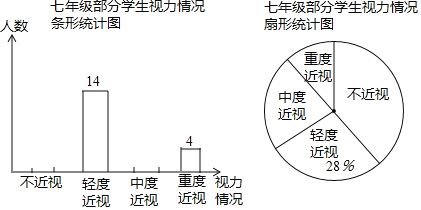
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图.在扇形统计图中,求“中度近视”对应扇形的圆心角的度数;
(3)若该校七年级学生有1200人,请你估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列命题:
①两组对角分别相等的四边形是平行四边形;
②一组对边平行,一组对角相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形;
⑤一组对边相等,一组对角相等的四边形是平行四边形,
(1)上述五个命题中,是真命题的是 (填写序号)
(2)请选择一个假命题,并举反例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
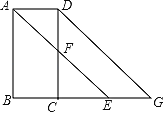
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() ,且
,且![]() 、
、![]() 位于原点两侧,与
位于原点两侧,与![]() 的正半轴交于
的正半轴交于![]() ,顶点
,顶点![]() 在
在![]() 轴右侧的直线
轴右侧的直线![]() :
:![]() 上,则下列说法:①
上,则下列说法:①![]() ②
②![]() ③
③![]() ④
④![]() 其中正确的结论有( )
其中正确的结论有( )

A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
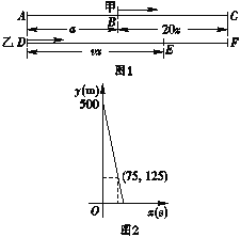
【题目】如图1所示,甲、乙两车沿直路同向行驶,车速分别为20 m/s和v(m/s),起初甲车在乙 车前a (m)处,两车同时出发,当乙车追上甲车时,两车都停止行驶.设x(s)后两车相距y (m),y与x的函数关系如图2所示.有以下结论:
①图1中a的值为500;
②乙车的速度为35 m/s;
③图1中线段EF应表示为![]() ;
;
④图2中函数图象与x轴交点的横坐标为100.
其中所有的正确结论是( )
A. ①④ B. ②③
C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com