
【题目】某校为了了解本校七年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对七年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中中度近视人数是不近视与重度近视人数之和的一半.
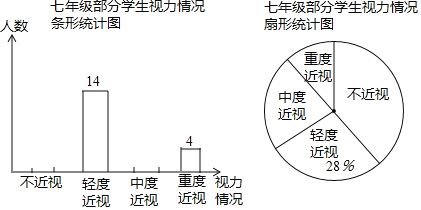
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图.在扇形统计图中,求“中度近视”对应扇形的圆心角的度数;
(3)若该校七年级学生有1200人,请你估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人?
【答案】(1)50(人);(2)图见解析,86.4°;(3)720
【解析】
(1)根据轻度近视的人数是14人,占总人数的28%,即可求得总人数;
(2)设中度近视的人数是x人,则不近视与重度近视人数的和为2x,列方程求得x的值,即可求得不近视的人数,然后利用360°乘以对应的百分比即可求得圆心角的度数;
(3)利用总人数乘以对应的百分比即可求解.
解:(1)本次调查的学生人数为14÷28%=50(人);
(2)设中度近视的人数是x人,则不近视与重度近视人数的和为2x,则x+2x+14=50,
解得:x=12,
则中度近视的人数是12,不近视的人数是:24﹣4=20(人),
所以“中度近视”对应扇形的圆心角度数是:360°×![]() =86.4°;
=86.4°;
补全条形图如下:
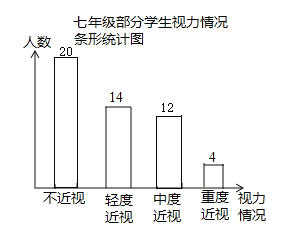
(3)估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有
1200×![]() =720(人).
=720(人).


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD(AB<AD)沿BD折叠后,点C落在点E处,且BE交AD于点F,若AB=4,BC=8.

(1)求DF的长;
(2)求△DBF和△DEF的面积;
(3)求△DBF中F点到BD边上的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传2022年北京﹣张家口冬季奥运会,小王在网上销售一种成本为20元/件的本届冬季奥运会宣传文化衫,销售过程中的其他各种费用(不再含文化衫成本)总计50(百元),有关销售量y(百件)与销售价格x(元/件)的相关信息如下:
销售量y(百件) | y=﹣0.1x+8 | y= |
销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
(1)求销售这种文化衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD= ______ ∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
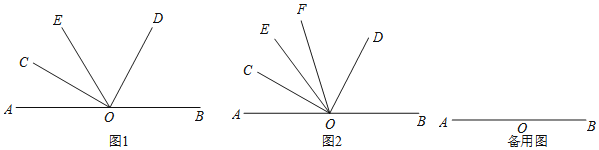
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分) 2011年5月上旬,无锡市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根
据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D
表示)四个等级进行统计,并绘制成如图所示的扇形图和统计表:
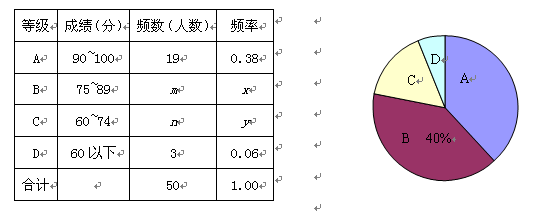
请你根据以上图表提供的信息,解答下列问题:
【1】(1) m= ,n= ,x= ,y= ;
【2】(2)在扇形图中,C等级所对应的圆心角是 度;
【3】(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】|a|+|b|=|a+b|,则a,b关系是( )
A. a,b的绝对值相等
B. a,b异号
C. a+b的和是非负数
D. a、b同号或a、b其中一个为0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),
上一动点(不与B,C重合),
求证:![]() PA=PB+PC.
PA=PB+PC.

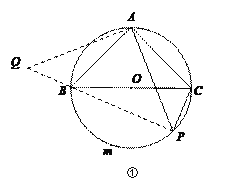
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
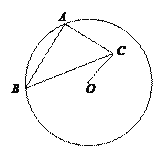
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.

(3)拓展延伸
如图,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com