
【题目】如图,将矩形ABCD(AB<AD)沿BD折叠后,点C落在点E处,且BE交AD于点F,若AB=4,BC=8.

(1)求DF的长;
(2)求△DBF和△DEF的面积;
(3)求△DBF中F点到BD边上的距离.
【答案】(1)5;(2)S△DBF =10,S△DEF=6;(3)F到BD边上的距离为![]() .
.
【解析】
(1)易证BF=FD,在直角△ABF中,根据勾股定理就可以求出DF的长;
(2)由折叠的性质得BE=BC=8,DE=CD=4,∠E=90°,EF=BE﹣BF=3,由S△DEF![]() EFDE,S△DBF=S△BDE﹣S△DEF即可得出结果;
EFDE,S△DBF=S△BDE﹣S△DEF即可得出结果;
(3)由勾股定理得出BD的长,设F到BD边上的距离为h,则S△DBF![]() BDh,即可得出结果.
BDh,即可得出结果.
(1)∵四边形ABCD是矩形,∴AD=BC=8,AB=CD=4,∠A=90°,AD∥BC,∴∠DBC=∠FDB,由折叠性质得:∠DBC=∠DBE,∴∠FDB=∠FBD,∴BF=FD,设AF=x,则BF=DF=8﹣x.在Rt△ABF中,由勾股定理得:AB2+AF2=BF2,即:42+x2=(8﹣x)2,解得:x=3,∴DF=8﹣3=5;
(2)由折叠的性质得:BE=BC=8,DE=CD=4,∠E=90°,EF=BE﹣BF=8﹣5=3,∴S△DEF![]() EFDE
EFDE![]() 3×4=6,S△DBF=S△BDE﹣S△DEF
3×4=6,S△DBF=S△BDE﹣S△DEF![]() BEDE﹣6
BEDE﹣6![]() 8×4﹣6=10;
8×4﹣6=10;
(3)BD![]() 4
4![]() ,设F到BD边上的距离为h,则S△DBF
,设F到BD边上的距离为h,则S△DBF![]() BDh,即:10
BDh,即:10![]() 4
4![]() h,解得:h
h,解得:h![]() ,∴F到BD边上的距离为
,∴F到BD边上的距离为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点![]() ,
,![]() ,
,![]() 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的![]() 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数![]() ,当
,当![]() 取值
取值![]() 和
和![]() 时,函数值分别为
时,函数值分别为![]() ,
,![]() ,故
,故![]() ,因此函数
,因此函数![]() 是限减函数,它的限减系数为
是限减函数,它的限减系数为![]() .
.
(1)写出函数![]() 的限减系数;
的限减系数;
(2)![]() ,已知
,已知![]() (
(![]() )是限减函数,且限减系数
)是限减函数,且限减系数![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)已知函数![]() 的图象上一点
的图象上一点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,将函数
轴,将函数![]() 的图象在点
的图象在点![]() 右侧的部分关于直线
右侧的部分关于直线![]() 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
![]()
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速铁路(简称高铁),是指通过改造原有线路(直线化、轨距标准化),使最高营运速度达到不小于每小时200千米,或者专门修建新的“高速新线”,使营运速率达到每小时250公里以上的铁路系统。宜春距离上海960千米,据了解高铁的平均速度比动车的平均速度每小时快96千米,从上海到宜春坐动车需要的时间是坐高铁需要时间的1.8倍。
(1)根据上面信息,请你求出上海到宜春高铁和动车的平均速度。
(2)广州距北京1800千米,以这样的平均速度坐高铁从广州到北京需要多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中, M为BC边上的中点, D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE.
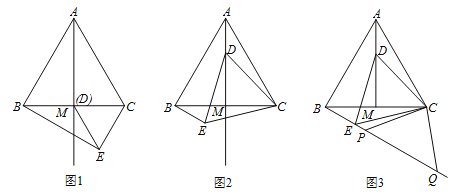
(1)填空:若D与M重合时(如图1)∠CBE= 度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(2)的条件下,如图3,若点P、Q在BE的延长线上,且CP=CQ=4,AB=6,试求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
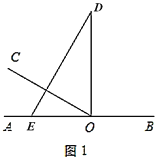
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周,如图2,经过
的速度沿顺时针方向旋转一周,如图2,经过![]() 秒后,
秒后,![]() 恰好平分
恰好平分![]() .
.
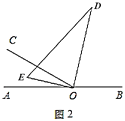
①此时![]() 的值为______;(直接填空)
的值为______;(直接填空)
②此时![]() 是否平分
是否平分![]() ?请说明理由.
?请说明理由.
(2)在(1)问的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
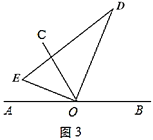
(3)在(2)问的基础上,经过多长时间![]() 平分
平分![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 两地相距
两地相距![]() km,甲、乙两人沿同一公路从
km,甲、乙两人沿同一公路从![]() 地出发到
地出发到![]() 地,甲骑摩托车,乙骑电动车,图中直线
地,甲骑摩托车,乙骑电动车,图中直线![]() ,
,![]() 分别表示甲、乙离开
分别表示甲、乙离开![]() 地的路程
地的路程![]() (km)与时问
(km)与时问![]() (h)的函数关系的图象.根据图象解答下列问题.
(h)的函数关系的图象.根据图象解答下列问题.
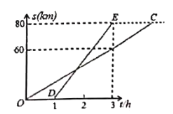
(1)甲比乙晚出发几个小时?乙的速度是多少?
(2)乙到达终点![]() 地用了多长时间?
地用了多长时间?
(3)在乙出发后几小时,两人相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份 | 2014 | 2015 | 2016 | 2017(预计) |
快递件总量(亿件) | 140 | 207 | 310 | 450 |
电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
查看答案和解析>>
科目:初中数学 来源: 题型:
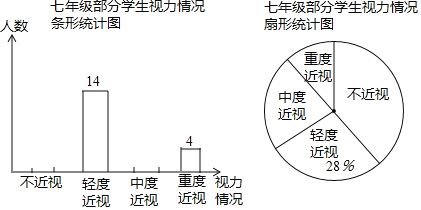
【题目】某校为了了解本校七年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对七年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中中度近视人数是不近视与重度近视人数之和的一半.
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图.在扇形统计图中,求“中度近视”对应扇形的圆心角的度数;
(3)若该校七年级学生有1200人,请你估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com