
【题目】综合题
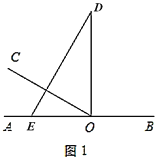
如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周,如图2,经过
的速度沿顺时针方向旋转一周,如图2,经过![]() 秒后,
秒后,![]() 恰好平分
恰好平分![]() .
.
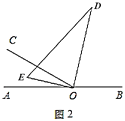
①此时![]() 的值为______;(直接填空)
的值为______;(直接填空)
②此时![]() 是否平分
是否平分![]() ?请说明理由.
?请说明理由.
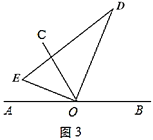
(2)在(1)问的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
(3)在(2)问的基础上,经过多长时间![]() 平分
平分![]() ?
?
【答案】(1)①3;②是,理由见解析;(2)经过5秒或69秒时,![]() 平分
平分![]() ;(3)经过
;(3)经过![]() 秒时,
秒时,![]() 平分
平分![]() .
.
【解析】
(1)①先求出![]() 时的
时的![]() 的度数,再求出当
的度数,再求出当![]() 恰好平分
恰好平分![]() 时
时![]() ,最后根据旋转的角度等于前后两次所求
,最后根据旋转的角度等于前后两次所求![]() 度数的差列出方程即得.
度数的差列出方程即得.
②在①中求出的![]() 的条件下,求出此时的
的条件下,求出此时的![]() 的度数即可.
的度数即可.
(2)先根据![]() 平分
平分![]() 可将
可将![]() 旋转度数与三角板旋转度数之差分为
旋转度数与三角板旋转度数之差分为![]() 、
、![]() 和
和![]() 三种情况, 然后以
三种情况, 然后以![]() 平分
平分![]() 为等量关系列出方程即得.
为等量关系列出方程即得.
(3)先根据![]() 旋转速度与三角板旋转速度判断
旋转速度与三角板旋转速度判断![]() 平分
平分![]() 应该在两者旋转过
应该在两者旋转过![]() 之后,然后用
之后,然后用![]() 分别表示出
分别表示出![]() 与
与![]() 的度数,最后依据
的度数,最后依据![]() 平分
平分![]() 为等量关系列出方程即可.
为等量关系列出方程即可.
(1)①当![]() 时
时
∵![]() ,
,![]()
∴![]()
当直角三角板绕![]() 点旋转
点旋转![]() 秒后
秒后
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() 恰好平分
恰好平分![]()
∴![]()
∴![]()
∴![]() .
.
②是,理由如下:
∵转动3秒,∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 平分
平分![]() .
.
(2)直角三角板绕![]() 点旋转一周所需的时间为
点旋转一周所需的时间为![]() (秒),射线
(秒),射线![]() 绕
绕![]() 点旋转一周所需的时间为
点旋转一周所需的时间为
![]() (秒),
(秒),
设经过![]() 秒时,
秒时,![]() 平分
平分![]() ,
,
由题意:①![]() ,
,
解得:![]() ,
,
②![]() ,
,
解得:![]() ,不合题意,
,不合题意,
③∵射线![]() 绕
绕![]() 点旋转一周所需的时间为
点旋转一周所需的时间为![]() (秒),45秒后停止运动,
(秒),45秒后停止运动,
∴![]() 旋转
旋转![]() 时,
时,![]() 平分
平分![]() ,
,
∴![]() (秒),
(秒),
综上所述,![]() 秒或69秒时,
秒或69秒时,![]() 平分
平分![]() .
.
(3)由题意可知,![]() 旋转到与
旋转到与![]() 重合时,需要
重合时,需要![]() (秒),
(秒),
![]() 旋转到与
旋转到与![]() 重合时,需要
重合时,需要![]() (秒),
(秒),
所以![]() 比
比![]() 早与
早与![]() 重合,
重合,
设经过![]() 秒时,
秒时,![]() 平分
平分![]() .
.
由题意:![]() ,
,
解得:![]() ,
,
所以经过![]() 秒时,
秒时,![]() 平分
平分![]() .
.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
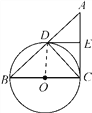
【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
(1)求证:DE是⊙O的切线;
(2)若BD=4,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
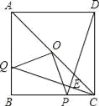
【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地休闲广场落成,吸引了很多人前往锻炼游玩,某校数学小组统计了“五一”期间在广场休闲的人员分布情况,统计图如下:
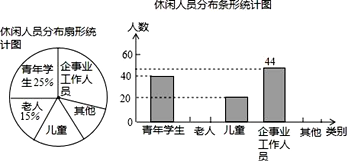
(1)求统计的这段时间内到广场休闲的总人数及老人人数.
(2)求休闲人员扇形统计图中“其他”人员项目所对应扇形的圆心角度数,并将条形统计图补充完整.
(3)根据以上数据,能否估计一年中(以365天计)到该广场休闲的人数?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD(AB<AD)沿BD折叠后,点C落在点E处,且BE交AD于点F,若AB=4,BC=8.

(1)求DF的长;
(2)求△DBF和△DEF的面积;
(3)求△DBF中F点到BD边上的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 从
从![]() 点出发,以
点出发,以![]() 秒的速度沿折线
秒的速度沿折线![]() 匀速运动,到
匀速运动,到![]() 点停止运动,设
点停止运动,设![]()
![]() 的面积为
的面积为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒.
秒.

(1)点![]() 运动到点
运动到点![]() ,
,![]() = .点
= .点![]() 运动到点
运动到点![]() ,
,![]() = .
= .
(2)请你用含![]() 的式子表示y.
的式子表示y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com